Chia hai lũy thừa cùng cơ số, định nghĩa, công thức và bài tập

Lũy thừa là gì? Cơ số là gì? Công thức chia hai lũy thừa cùng cơ số, ví dụ cụ thể và các bài tập vận dụng từ cơ bản đến nâng cao.

Chia hai lũy thừa cùng cơ số là một khái niệm có ứng dụng rộng rãi trong toán học cũng như trong đời sống hằng ngày. Nó giúp ta đơn giản hóa các phép tính, rút gọn biểu thức và giải các dạng bài toán liên quan đến lũy thừa. Đặc biệt trong toán đại số chương trình toán lớp 6 và toán ở bậc trung học cơ sơ, chia hai lũy thừa cùng cơ số là một phép tính quan trọng để áp dụng với các biểu thức đa thức và hàm số.

Trong bài viết này, hãy cùng thayphu khám phá định nghĩa, công thức tính và các bài tập vận dụng và ôn tập của dạng toán này nhé.

Định nghĩa lũy thừa cùng cơ số

Lũy thừa là gì?

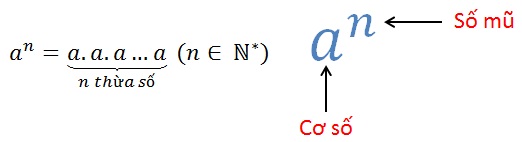
Lũy thừa là một phép tính mà trong đó một số được nhân với chính nó một số lần. Nó được biểu diễn dưới dạng an, trong đó a là cơ số và n là chỉ số mũ.

Ví dụ, trong phép tính 23. Phép tính này có thể hiểu là "nhân số 2 với chính nó ba lần". Kết quả của phép tính 2^3 là 8, bởi vì 2 × 2 × 2 = 8.

Cơ số là gì?

Cơ số là số được nhân với chính nó trong phép tính lũy thừa. Trong một phép lũy thừa có dạng an, a được gọi là cơ số.

Ví dụ, trong phép tính 23:

Số 2 được gọi là cơ số.

Số 3 được gọi là chỉ số mũ.

Cơ số có thể là bất kỳ số nguyên, số thực hoặc số phức, tùy thuộc vào loại phép tính và ngữ cảnh sử dụng. Trong toán học, các cơ số phổ biến nhất là các số tự nhiên (1, 2, 3, ...), số nguyên (0, ±1, ±2, ...), số thực (bao gồm các số thập phân) và số phức (bao gồm phần thực và phần ảo).

Công thức chia hai lũy thừa cùng cơ số

Khi chia hai lũy thừa cùng cơ số, ta giữ cơ số không đổi và lấy số mũ của số bị chia trừ số mũ của số chia.

Công thức tổng quát:

am : an = am-n (a ≠ 0, m > n).

Cách thực hiện chia hai lũy thừa cùng cơ số:

• Xác định cơ số của lũy thừa.
• Trừ số mũ của lũy thừa chia từ chỉ số mũ của lũy thừa bị chia.
• Kết quả là lũy thừa mới với cùng cơ số và số mũ là hiệu của phép tính đã tính.

Ví dụ: Hãy thực hiện phép tính sau

56 : 53

Ta có:

56 = 5 × 5 × 5 × 5 × 5 × 5

53 = 5 × 5 × 5

⇔

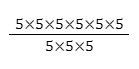
= 5 × 5 × 5 = 56 - 3 = 53

Vậy suy ra: 56 : 53 = 56 - 3 = 53.

Lưu ý: a0 = 1 (a ≠ 0).

Bài tập vận dụng và ôn tập

Bài tập 1: Thực hiện các phép tính sau

1. 117 : 112
2. 259 : 253
3. 98 : 94 : 92
4. 1445 : 1441

Gợi ý lời giải:

1. 117 : 112

= 117 - 2 = 115

2. 259 : 253

= 259 - 3 = 256

3. 98 : 94 : 92

= 98 - 4 - 2 = 92

4. 1445 : 1441

= 1445 - 1 = 1444

Bài tập 2: Trong các số đã cho dưới đây, hãy sắp xếp chúng thành các lũy thừa cùng cơ số.

2, 36, 8, 125, 66, 52, 33, 9, 4, 6, 73, 49, 43, 16, 3, 81.

Gợi ý lời giải:

Ta đưa các số đã cho về dạng lũy thừa như sau:

36 = 62, 8 = 23, 125 = 53, 9 = 32, 4 = 22, 49 = 72, 16 = 42, 81= 92

Từ đó suy ra ta có thể sắp xếp như sau:

Cùng cơ số 2: 2, 4, 43, 8, 16

Cùng cơ số 3: 3, 33, 9, 81

Cùng cơ số 5: 52, 125

Cùng cơ số 6: 6, 66, 36

Cùng cơ số 7: 73, 49

Bài tập 3: Tìm x:

1. 64.x = 610
2. 235.x -236 = 0
3. 5.(x - 3) 53 = 0

Gợi ý lời giải:

1. 64.x = 610

x = 610 : 64

x = 610 - 4

x = 66

2. 235.x - 236 = 0

x = 236 : 235

x= 236 - 5 = 23

3. 5.(x - 3) - 53 = 0

5.(x - 3) = 53

x - 3 = 53 - 1 = 52 = 25

x = 25 - 3 = 22

Bài tập 4: So sánh các số sau

1. 515 : 510 và 3000

2. 173 : 17 và 17

3. 38 : 33 và 256

4. 1024 và 220 : 210

Gợi ý lời giải:

1. 515 : 510 và 3000

Ta có: 515 : 510 = 515 - 10 = 55 = 3125

Mà 3125 > 3000

Vậy 515 : 510 > 3000

2. 173 : 17 và 17

Ta có: 173 : 17 = 173 - 1 = 172 > 17

Vậy 173 : 17 > 17

3. 38 : 33 và 256

Ta có: 38 : 33 = 38 - 3 = 35 = 243

Mà 243 < 256

Vậy 38 : 33 < 256

4. 1024 và 220 : 210

Ta có: 220 : 210 = 220 - 10 = 210 = 1024

Vậy 1024 và 220 : 210

Chia hai lũy thừa cùng cơ số là một dạng toán nền tảng của chương trình toán bậc trung học cơ sở, đặc biệt là chương trình toán lớp 6. Đây là dạng toán khá thú vị vì nó có rất nhiều dạng bài tập khác nhau. Ngoài ra, nó cũng là kiến thức cơ bản để giải các bài toán nâng cao hơn. Vì vậy, hãy ôn tập thật nhiều để có thể nắm vững công thức và phương pháp giải dạng toán chia hai lũy thừa này nhé, vì nó sẽ giúp chúng ta tiết kiệm rất thời gian và tránh sai sót ở các lỗi cơ bản khi giải đề và làm các bài tập liên quan.