Cách tính độ dài đường phân giác trong tam giác và bài tập

Tính độ dài đường phân giác trong tam giác là đoạn thẳng nối một đỉnh của tam giác với điểm trung điểm của cạnh đối diện tạo thành một tam giác.

Đường phân giác của một góc là một khái niệm quan trọng trong hình học tam giác và đóng vai trò quan trọng trong việc xác định các tính chất cũng như mối quan hệ trong các tam giác. Khi học cách tính độ dài đường phân giác của một góc, chúng ta có được cái nhìn tổng quan rõ ràng hơn về cấu trúc và tính chất của hình tam giác. Trong bài viết này chúng ta hãy cùng thayphu khám phá cách tính độ dài đường phân giác của một góc và cách áp dụng nó vào các bài toán hình học tam giác.

Định nghĩa về đường phân giác trong tam giác

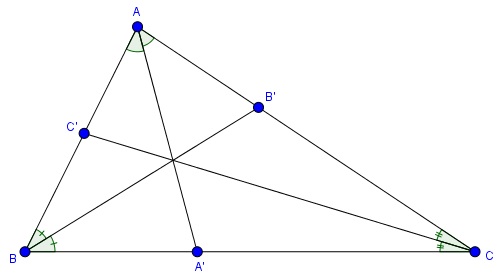
Định nghĩa về đường phân giác trong tam giác

Đường phân giác của một tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Mỗi tam giác có ba đường phân giác, mỗi đường phân giác bắt đầu từ một đỉnh và kết thúc tại trung điểm cạnh đối diện.

Vai trò của đường phân giác

Chúng đóng vai trò quan trọng trong việc xác định các tính chất và mối quan hệ trong tam giác.

Đường phân giác có thể tìm được điểm chung với các đường thẳng khác của tam giác như đường đồng mức, đường tâm hoặc đường trực giao.

Giao điểm của ba đường phân giác của một tam giác gọi là trọng tâm của tam giác.

Trọng tâm là một điểm quan trọng trong một tam giác vì nó có nhiều tính chất đặc biệt và đóng vai trò quan trọng trong các bài toán hình học, tính toán liên quan đến tam giác.

Tính chất của đường phân giác trong tam giác

Đường phân giác của một tam giác có một số tính chất quan trọng:

• Chia tam giác thành hai phần có diện tích bằng nhau: Đường phân giác chia tam giác thành hai phần có diện tích bằng nhau. Điều này có nghĩa là diện tích của tam giác chia cho đường phân giác của góc sẽ đối xứng với đường phân giác của góc.
• Tìm điểm chung với các đường thẳng trong tam giác: Đường phân giác của góc có thể tìm được điểm chung với các đường thẳng trong tam giác khác như đường cao, đường trung tuyến, đường thẳng trung trực.Ví dụ, đường phân giác của một đỉnh cắt chiều cao của đỉnh đối diện tại tâm.
• Giao điểm của ba đường phân giác là trọng tâm: Ba đường phân giác của một tam giác cắt nhau tại một điểm gọi là tâm của tam giác. Trọng tâm là trung điểm của các đoạn thẳng nối đỉnh của tam giác với trung điểm của cạnh đối diện.
• Độ dài đường phân giác và tính chất của tam giác: Độ dài của đường phân giác có thể liên quan đến các tính chất khác của tam giác, chẳng hạn như độ dài các cạnh, kích thước của các góc hoặc tỷ lệ khung hình.

Công thức tính đường phân giác trong tam giác

Để tính độ dài đường phân giác trong tam giác, chúng ta có thể sử dụng các công thức và quy tắc phụ thuộc vào thông tin đã biết về tam giác. Dưới đây là các công thức phổ biến để tính đường phân giác trong tam giác:

Công thức chính để tính độ dài đường phân giác trong tam giác là công thức đường phân giác từ một đỉnh. Dưới đây là công thức chi tiết:

Đường phân giác từ một đỉnh (đường phân giác từ đỉnh A):

$g_a = \frac{2}{BC} \times \sqrt{bcs(s-a)}$

Trong đó:

• $g_a$ là độ dài đường phân giác từ đỉnh A.
• BC là độ dài cạnh đối diện với đỉnh A.
• s là nửa chu vi tam giác ($s = \frac{AB + BC + CA}{2}$).
• a là độ dài đường cao từ đỉnh A.

Ngoài ra, còn một số công thức khác có thể được sử dụng trong các trường hợp cụ thể, chẳng hạn như công thức Heron để tính diện tích tam giác và công thức tính đường phân giác trong tam giác vuông hoặc tam giác đều.

Một số dạng toán khi tính đường phân giác trong tam giác

Khi tính độ dài đường phân giác trong tam giác, có một số dạng toán thường gặp. Dưới đây là một số ví dụ về các dạng toán phổ biến liên quan đến tính đường phân giác trong tam giác:

Dạng 1:Tính độ dài đường phân giác trong tam giác vuông

Trong tam giác vuông, đường phân giác từ đỉnh góc vuông đến trung điểm của cạnh đối diện là nửa đường cao của tam giác. Vì vậy, để tính độ dài đường phân giác trong tam giác vuông, bạn có thể sử dụng các quy tắc liên quan đến ba cạnh tam giác vuông, chẳng hạn như định lý Pythagoras.

Dạng 2:Tính độ dài đường phân giác trong tam giác đều

Trong tam giác đều, tất cả các cạnh và góc đều có giá trị như nhau. Đường phân giác trong tam giác đều cắt nhau tại một điểm duy nhất và chia tam giác thành hai phần bằng nhau. Đối với tam giác đều, độ dài của đường phân giác bằng độ dài một cạnh nhân với một hệ số xác định

Dạng 3:Tính độ dài đường phân giác trong tam giác không vuông

Trong các tam giác không vuông, tính độ dài đường phân giác phụ thuộc vào thông tin đã biết, chẳng hạn như độ dài các cạnh và góc tam giác. Bạn có thể sử dụng các quy tắc hình học như định lý cosin và định lý sin để tính độ dài đường phân giác trong tam giác không vuông.

Một số lưu ý khi tính độ dài đường phân giác

Dưới đây là một số lưu ý bạn cần nắm khi tính độ dài đường phân giác

• Đối với công thức tính đường phân giác của một đỉnh cần lưu ý các biểu thức trong dấu căn phải là diện tích hình tam giác.
• Do đó, phải sử dụng độ dài các cạnh và nửa chu vi để tính diện tích chính xác của tam giác
• Trong trường hợp tam giác vuông đường phân giác của góc bằng chiều cao của tam giác vuông góc và độ dài đường phân giác của góc bằng nửa cạnh huyền
• Các đường phân giác của một tam giác đều là các đường thẳng cắt nhau tại một điểm gọi là tâm. Trọng tâm là trung điểm của các đoạn thẳng nối đỉnh với trung điểm của cạnh đối diện.
• Khi tính đường phân giác của một đỉnh của một tam giác, hãy nhớ rằng các đường phân giác của các đỉnh khác có cùng độ dài.
• Điều này có nghĩa là các đường phân giác của tam giác là những đường thẳng có độ dài bằng nhau.
• Đối với các tam giác không phải là góc vuông, việc sử dụng các công thức như chiều cao, đường trung tuyến,đường phân giác của góc có thể yêu cầu kiến thức về lượng giác hoặc các phương pháp tính toán khác.

Bài tập áp dụng

Bài 1:Trong tam giác vuông, đường cao từ đỉnh vuông góc chính là?

A) Cạnh huyền

B) Cạnh góc vuông

C) Cạnh còn lại

D) Đường tròn ngoại tiếp

Đáp án đúng :A) Cạnh huyền

Bài 2: Đường phân giác trong tam giác chia đôi góc tại đỉnh thành các góc bằng nhau.

A) Đúng

B) Sai

Đáp án đúng: B) Sai

Bài 3:Tam giác có ba đường cao đồng dạng

A) Đúng

B) Sai

Đáp án đúng: B) Sai

Bài 4: Trong tam giác vuông, đường phân giác từ đỉnh vuông góc chia cạnh huyền thành hai phần có tỉ lệ bằng độ dài các cạnh góc vuông nhỏ.

A) Đúng

B) Sai

Đáp án đúng: A) Đúng

Bài 5: Trọng tâm của tam giác là trung điểm của các đoạn thẳng nối đỉnh với trung điểm của cạnh đối diện.

A) Đúng

B) Sai

Đáp án đúng: A) Đúng

Kết luận

Hy vọng rằng những bài tập tự luận và câu hỏi trắc nghiệm về hình học tam giác đã giúp bạn ôn tập và nắm vững kiến thức cơ bản về cách tính đường phân giác trong tam giác.Nếu bạn cần thêm thông tin hoặc có bất kỳ câu hỏi nào khác, hãy liên hệ với chúng tôi.