Bất phương trình bậc nhất một ẩn, cách giải và bài tập ứng dụng

Phương pháp giải bất phương trình bậc nhất một ẩn. Các quy tắc, ứng dụng thú vị và cách biểu diễn bất phương trình trên trục số cực hay.

Bất phương trình bậc nhất một ẩn là một khái niệm tuy cơ bản nhưng quan trọng trong toán học và có nhiều ứng dụng trong thực tế. Bất phương trình bậc nhất một ẩn là một dạng phương trình chứa một biến số duy nhất và biểu thị một khoảng giá trị của biến số đó trên trục số.

Đây là một khái niệm tuy mới trong chương trình toán 8 và chúng ta cần nắm rõ. Vì vậy, trong bài viết này, thayphu sẽ giới thiệu về bất phương trình này cùng các phương pháp giải và ứng dụng của nó trong các vấn đề thực tế.

Định nghĩa bất phương trình bậc nhất một ẩn?

Bất phương trình bậc nhất 1 ẩn.

Bất phương trình bậc nhất 1 ẩn là bất phương trình có dạng: ax + b > 0 ( hay ax + b < 0, ax + b ≤ 0, ax + b ≥ 0). Trong đó, a ≠ 0, a và b là các hằng số đã cho, x là biến số cần tìm.

Ví dụ: các bất phương trình có dạng

3x + 4 ≤ 0

7x - 8 > 0

Các quy tắc để chuyển đổi một bất phương trình

Tương tự như phương trình bậc nhất 1 ẩn thì bất phương trình cũng có các quy tắc gần giống để giải bài toán. Ở dạng bất phương trình bậc nhất 1 ẩn ta có 2 quy tắc như sau:

Quy tắc 1: Chuyển vế của hạng tử

Khi ta chuyển một số từ vế này sang vế khác của dấu bằng, ta phải đổi dấu của số hạng đó. Ví dụ, nếu ta chuyển +a sang vế khác của dấu bằng, nó sẽ trở thành -a.

Ví dụ: Giải phương trình sau: x - 4 = 0

⇔ x = 4 ( -4 đổi sang vế khác thì đổi dấu thành +4)

Quy tắc 2: Nhân hoặc chia các hạng tử với một số

Khi nhân hoặc chia cả hai vế với một số khác không, tính đẳng thức của bất phương trình được giữ nguyên và giá trị của bất phương trình sau khi nhân hoặc chia có thể thay đổi.

Tuy nhiên, dạng bất phương trình khác với dạng phương trình ở chỗ:

• Khi nhân hoặc chia hai vế cho cùng 1 số dương thì dấu của bất phương trình giữ nguyên.
• Khi nhân hoặc chia hai vế cho cùng 1 số âm thì dấu của bất phương trình sẽ đổi chiều.

Ví dụ 1: Giải bất phương trình sau: 5x - 8 ≤ 2

⇔ 5x ≤ 2 + 8 (chuyển vế đổi dấu)

⇔ 5x ≤ 10 (chia cả hai vế cho 5 hoặc nhân cho ⅕)

⇔ x ≤ 2 (ở đây ta chia cả 2 vế cho cùng 1 số dương là 5 nên bất phương trình không đổi dấu)

Vậy x ≤ 2 là nghiệm của bất phương trình.

Ví dụ 2: Giải bất phương trình sau: -7x + 25 > 4

⇔ -7x > 4 - 25 (chuyển vế đổi dấu)

⇔ -7x > -21 (chia cả hai vế cho -7)

⇔ x < 3 (ở đây ta chia cả 2 vế cho cùng 1 số âm là -7 nên bất phương trình đổi dấu)

⇔ Vậy x < 3 là nghiệm của bất phương trình.

Các lưu ý cần nắm

• Bất phương trình bậc nhất một ẩn khác với phương trình bậc nhất một ẩn ở chỗ nó không yêu cầu biến số x phải đạt giá trị duy nhất, mà chỉ cần thỏa mãn một phạm vi giá trị nào đó.
• Khi giải bất phương trình bậc nhất một ẩn, ta cần chú ý tới các điều kiện xác định và giới hạn của nghiệm

Phương pháp giải bất phương trình bậc nhất một ẩn

Để giải được dạng toán bất phương trình này, ta chỉ cần áp dụng hai quy tắc đã nói ở trên vào bài toán, ta sẽ giải được bất phương trình. Ta thực hiện các bước như sau:

• Bước 1: Đưa bất phương trình về dạng chuẩn

Chúng ta cần đảm bảo rằng biến số x chỉ xuất hiện ở một bên của bất phương trình và hệ số của x nằm về phía còn lại. Nói cách khác, ta sẽ đưa bất phương trình về dạng ax + b < 0 hoặc ax + b > 0, trong đó a và b là các hằng số.

• Bước 2: Áp dụng các quy tắc biến đổi bất phương trình

Sau khi đưa về dạng chuẩn, chúng ta có thể áp dụng các quy tắc biến đổi bất phương trình như đã giới thiệu ở trên để tìm phạm vi giá trị của biến số x.

• Bước 3: Xác định phạm vi giá trị của x

Dựa trên các quy tắc biến đổi đã áp dụng, ta có thể xác định phạm vi giá trị của biến số x. Từ đó, ta sẽ biết x nằm trong khoảng nào.

• Bước 4: Tìm nghiệm và đáp án

Với phạm vi giá trị đã xác định, ta có thể tìm các giá trị cụ thể của x mà thỏa mãn bất phương trình. Nếu phạm vi là một khoảng liên tục, ta có thể đưa ra đáp án dưới dạng một khoảng giá trị.

Ví dụ: Giải bất phương trình sau: 2x/3 + 6 > 2

⇔ 2x/3 + 6 > 9 (chia cả 2 vế cho 3 đề đưa về dạng ax + b > 0)

⇔ 2x + 2 > 3

⇔ 2x > 1

⇔ x > ½

Vậy x < 3 là nghiệm của bất phương trình.

Cách biểu diễn một bất phương trình trên trục số

Biểu diễn 1 bất phương trình trên trục số là 1 kỹ năng quan trọng trong toán học mà chúng ta cần nắm. Sau đây là các kiến thức cần nắm:

• Bước 1: Vẽ trục số (tham khảo hình minh họa)
• Bước 2: Thể hiện bất phương trình trên trục số

Ví dụ: Chúng ta cần biết được giá trị của bất phương trình x - 1 > 7 nằm ở đâu trên trục số. Giải bpt ta có giá trị x > 8

• Nếu dấu của bpt là > thì ta vẽ dấu ngoặc đơn về phía bên phải, biểu thị ta nhận các giá trị lớn hơn và gạch chéo các giá trị bên trái.
• Ngược lại, nếu dấu của bpt là < thì ta vẽ dấu ngoặc đơn về phía bên trái, biểu thị ta nhận các giá trị nhỏ hơn và gạch chéo các giá trị bên phải.
• Ngoài ra, nếu dấu của bpt là ≤ hoặc ≥ thì ta sẽ sử dụng dấu ngoặc vuông thay cho dấu ngoặc đơn, và nguyên lý cũng tương tự ngoặc đơn.

Ứng dụng của bất phương trình bậc nhất một ẩn

Kinh tế: Bất phương trình bậc nhất được sử dụng để mô hình hóa và giải quyết các vấn đề liên quan đến tài chính và kinh tế. Ví dụ, nó có thể được sử dụng để xác định phạm vi giá trị của biến số trong các mô hình tài chính và kinh doanh, như phạm vi giá trị của sản phẩm hoặc dịch vụ để đảm bảo lợi nhuận.

Địa lý và môi trường: Trong lĩnh vực địa lý và môi trường, bất phương trình bậc nhất một ẩn có thể được sử dụng để mô hình hóa và giải quyết các vấn đề liên quan đến sự phân bố và sử dụng tài nguyên, như sự phân phối của nước, năng lượng hoặc đất đai.

Xã hội học: Ngoài ra, nó còn có thể được áp dụng trong xã hội học để nghiên cứu và phân tích các vấn đề xã hội. Ví dụ, nó có thể được sử dụng để nghiên cứu và đánh giá các yếu tố ảnh hưởng đến sự phân bố tài nguyên, thu nhập hoặc cơ hội trong xã hội.

Bài tập trắc nghiệm tự ôn luyện

Bài 1: Cho bpt như sau, giải bpt và tính xem có bao nhiêu nghiệm nguyên lớn hơn -10.

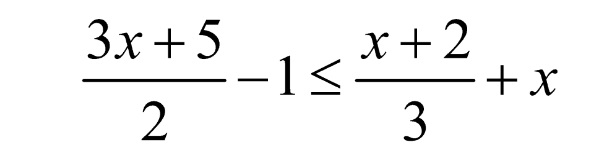
1. 4
2. 5
3. 7
4. 10

Đáp án: B

Bài 2: Giải bất phương trình sau: 4x + 4 > 3(x + 7)

1. x > 17
2. x < 6
3. x > 8
4. x > 15

Đáp án: A

Bài 3: Bất phương trình nào sau đây là bất phương trình một ẩn?

1. x^2 > 5
2. x^3 + x < 4
3. 2x + 5 > 0
4. 0x - 11 < 7

Đáp án: C

Kết luận

Qua bài viết trên, thayphu hy vọng các bạn đã nắm rõ được phương pháp để giải bất phương trình đúng và nhanh nhất. Bất phương trình là dạng toán tuy mới mẻ với học sinh lớp 8 nhưng là kiến thức nền tảng quan trọng cho sau này. Vì vậy các bạn hãy ôn luyện thật tốt để nắm vững dạng kiến thức vô cùng thú vị này nhé.