Đồ thị hàm số bậc nhất, lý thuyết, phương pháp và bài tập

Làm thế nào để vẽ đồ thị của hàm số bậc nhất? Tính chất, hệ số góc và các mẹo vẽ đồ thị nhanh.Các dạng toán thú vị của đồ thị hàm số.

Trong chương trình toán học ở cấp trung học cơ sở, các bạn học sinh sẽ được tìm hiểu và làm quen về một khái niệm rất thú vị đó là đồ thị của hàm số bậc nhất. Thế nhưng đồ thị của hàm số bậc nhất là gì? Các tính chất, phương pháp và bài tập của nó như thế nào? Hãy cùng thayphu tìm hiểu những kiến thức này thông qua bài viết này nhé.

Kiến thức về đồ thị hàm số bậc nhất cần nắm

Định nghĩa

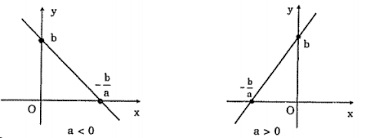
Đồ thị của hàm số bậc nhất là một đường thẳng trên hệ trục tọa độ. Hình dạng của đường thẳng được xác định bởi hệ số a và hệ số b trong phương trình hàm số f(x) = ax + b.

Tính chất

• Đồ thị hàm số sẽ cắt trục tung tại điểm có tung độ bằng giá trị b.
• Nếu b ≠ 0 thì đồ thị song song với đường thẳng y = ax.
• Nếu b = 0 thì đồ thị trùng với y = ax.
• Điểm b trong phương trình còn được gọi là tung độ gốc của đường thẳng.

Hệ số góc

Trong mặt phẳng Oxy, hệ số góc của đồ thị hàm số bậc nhất là hệ số a trong phương trình hàm số f(x) = ax + b. Hệ số a xác định góc tạo bởi đường thẳng trên đồ thị với trục Ox, và ta quy định góc đó là góc α.

• Nếu hệ số a dương (a > 0), thì α < 90° hay góc tạo bởi đường thẳng và trục Ox là góc nhọn. Đường thẳng sẽ tăng từ trái qua phải trên đồ thị. Khi giá trị của biến x tăng, giá trị của hàm số f(x) cũng tăng.
• Nếu hệ số a âm (a < 0), thì α > 90° hay góc tạo bởi đường thẳng và trục Ox là góc tù. Đường thẳng sẽ giảm từ trái qua phải trên đồ thị. Khi giá trị của biến x tăng, giá trị của hàm số f(x) sẽ giảm.

Lưu ý: Hệ số góc cũng xác định tỷ lệ thay đổi giữa giá trị của biến phụ thuộc (giá trị của y) và biến độc lập (giá trị của x). Nếu a = 0, đồ thị sẽ là một đường thẳng ngang song song hoặc trùng với trục hoành Ox và hàm số sẽ không phụ thuộc vào biến độc lập.

Phương pháp vẽ đồ thị hàm số bậc nhất

Phương trình của đồ thị hàm số bậc nhất là f(x) = ax + b (với a ≠ 0), ta có:

Cách 1: Vẽ đồ thị khi b ≠ 0

• Bước 1: Muốn xác định được điểm cắt trục tung, ta đặt x = 0 và tính được giá trị của y.
• Bước 2: Muốn xác định điểm cắt trục hoành, ta đặt y = 0 rồi giải phương trình để tìm x.
• Bước 3: Vẽ đường thẳng của đồ thị hàm số bằng cách nối hai điểm đã xác định ở trục tung và trục hoành.

Nói cách khác, để vẽ đồ thị hàm số y = ax + b, ta cần xác định hai điểm A (0, b) và B (-b/a; 0) rồi nối 1 đường thẳng đi qua hai điểm A và B đã tìm được.

Cách 2: Vẽ đồ thị khi b = 0

Các bước để xác định các điểm của đồ thị cũng tương tự như khi b ≠ 0. Tuy nhiên, khi b ≠ 0, ta có thể xác định các điểm nhanh hơn như sau:

Khi b = 0 ta có phương trình dạng d: y = ax sẽ đi qua gốc tọa độ O (0; 0) và điểm A (1; a)

Từ đó, ta vẽ đường thẳng d đi qua hai điểm O (0; 0) và A (1; a). Đường thẳng d là đồ thị hàm số.

Ví dụ: Hãy vẽ đồ thị hàm số y = 2x - 3

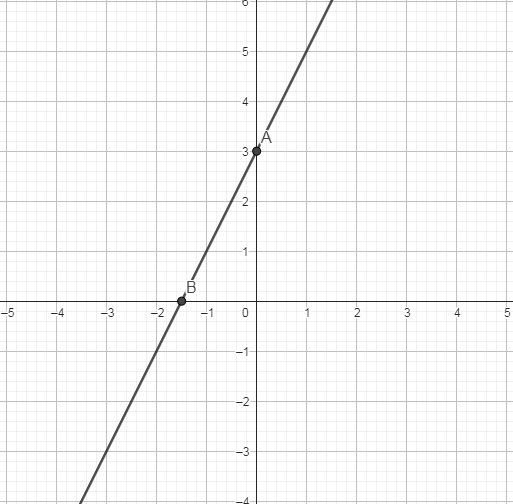
Với x = 0 thì y = -3 ⇒ Ta tìm được điểm A (0; -3).

Với y = 0 thì x = ⅔ ⇒ Ta tìm được điểm B (⅔; 0).

Nối 2 điểm A, B với nhau ta được một đồ thị như sau:

Các dạng bài tập thường gặp và bài tập vận dụng của đồ thị hàm số bậc nhất

Dạng 1: Vẽ đồ thị của hàm số bậc nhất

Phương pháp: Áp dụng phương pháp vẽ đồ thị hàm số đã nói như trên để giải dạng toán này.

Ví dụ: Vẽ các đồ thị hàm số sau trên cùng 1 mặt phẳng: y = x - 3, y = 3x - 3, y = -2x - 3. Ta có nhận xét gì về đồ thị của các hàm số đã cho.

Gợi ý lời giải:

Áp dụng phương pháp vẽ đồ thị hàm số, ta xác định được điểm giao của các hàm số với trục tung và trục hoành như sau:

y = x - 3 ⇒ A (3; 0), D (0; -3)

y = 3x - 3 ⇒ B (1; 0), D (0; -3)

y = -2x - 3 ⇒ C (-3/2; 0), D (0; -3)

Ta có đồ thị như hình sau:

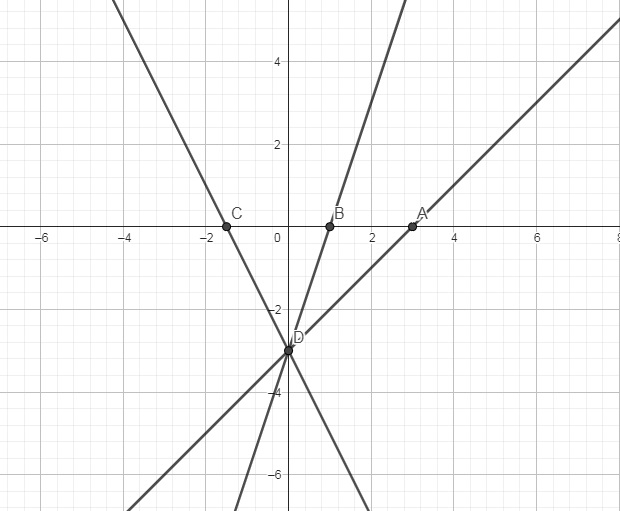
Từ đồ thị đã vẽ ở trên, ta có thể nhận xét cả 2 hàm số đều giao nhau tại cùng 1 điểm trên trục Oy là điểm D (0; -3).

Dạng 2: Xác định điểm đã cho có thuộc hay không thuộc đồ thị hàm số

Phương pháp:

Cách 1: Trên cùng 1 hệ trục tọa độ, ta vẽ đồ thị hàm số d: y = ax + b và điểm M.

• Nếu điểm M nằm trên đường thẳng d thì điểm đó thuộc đồ thị hàm số.
• Nếu điểm M không nằm trên đường thẳng d thì điểm đó không thuộc đồ thị hàm số.

Cách 2: Thay tọa độ điểm M(c, d) vào hàm số y = ax + b.

• Nếu ac + b = d thì M thuộc đồ thị hàm số
• Nếu ac + b ≠ d thì M không thuộc đồ thị hàm số.

Ví dụ: Hãy xác định hai điểm A (-⅓; 5), B(5/2; 2) có nằm trên đồ thị hàm số y = 3x + 4 đã cho không?

Gợi ý lời giải:

Thay x = -⅓ vào đồ thị hàm số ta được y = -⅓.(-3) + 4 = 5.

Vậy điểm A thuộc đồ thị hàm số y = -3x + 4.

Thay x = 5/2 vào đồ thị hàm số ta được y = 5/2.(-3) + 4 = -23/2

Vậy điểm B không thuộc đồ thị hàm số y = -3x + 4.

Kết luận

Qua bài viết trên, thayphu mong rằng các bạn đã nắm rõ được những kiến thức cơ bản về đồ thị của hàm số bậc nhất như định nghĩa, tính chất, hệ số góc hay các phương pháp để vẽ đồ thị hàm số nhanh. Có thể nói là một dạng toán cơ bản và quan trọng trong chương trình toán ở các trung học cơ sở. Vì vậy, các bạn hãy tích cực ôn luyện các dạng bài tập khác nhau để nắm vững dạng kiến thức tuy cơ bản nhưng cũng vô cùng thú vị này nhé.