Hàm số bậc nhất là gì? Tính chất quan trọng và bài tập

Hàm số bậc nhất là gì? Tính chất quan trọng và các dạng toán thường gặp của hàm số bậc nhất trong đề thi tuyển sinh vào 10 mà các em cần nắm.

Khi ta nói về hàm số bậc nhất, ta thường liên tưởng đến mối quan hệ giữa hai biến được biểu diễn bằng một đường thẳng đơn giản. Hàm số bậc nhất là một trong những khái niệm căn bản nhất trong toán học, thường xuyên xuất hiện trong các đề thi tuyển sinh vào 10.

Vì vậy, trong bài viết này, hãy cùng thayphu tìm hiểu như thế nào là hàm số bậc nhất cũng như các tính chất, ứng dụng thú vị của nó nhé. Đặc biệt còn cái cách dạng toán thường gặp và bài tập để chúng ta tự ôn luyện nữa.

Định nghĩa Hàm số bậc nhất

Định nghĩa về hàm số bậc nhất.

Hàm số bậc nhất, còn được gọi là hàm số tuyến tính, là một loại hàm số trong toán học có dạng chung là f(x) = ax + b. Trong đó, a và b là các hằng số và x là biến số. Trong hàm số bậc nhất, bậc của biến số là 1 và hệ số a khác 0.

Tính chất Hàm số bậc nhất

• Hàm số bậc nhất được xác định với mọi giá trị của x thuộc tập hợp R
• Hàm số bậc nhất có tính chất đồng biến và nghịch biến dựa vào hằng số a của hàm số:
• Nếu a > 0 ⇒ Hàm số đồng biến trên R
• Nếu a < 0 ⇒ Hàm số nghịch biến trên R
• Hệ số b trong phương trình hàm số xác định điểm cắt trục y, nghĩa là giá trị của hàm số khi x = 0. Điểm cắt trục y có tọa độ (0, b) trên đồ thị.
• Hàm số bậc nhất có một nghiệm duy nhất, vì nó là một hàm số tuyến tính. Nghiệm là giá trị của biến số x khi hàm số đạt giá trị bằng 0. Nghiệm của hàm số bậc nhất được tính bằng cách giải phương trình ax + b = 0, và nghiệm đó là x = -b/a.
• Hàm số bậc nhất có tính chất tuyến tính, nghĩa là nếu ta có hai giá trị x1 và x2, thì f(x1 + x2) = f(x1) + f(x2).
• Hai hàm số bậc nhất có cùng hệ số a nhưng khác nhau về hệ số b sẽ có đồ thị song song nhau trên mặt phẳng. Nếu hai hàm số có cùng cả hai hệ số a và b, thì đồ thị của chúng sẽ trùng nhau.

Tính biến thiên của hàm số bậc nhất

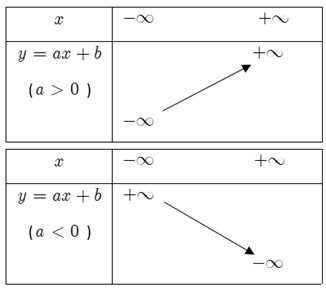
Biến thiên của hàm số bậc nhất được xác định dựa vào hệ số a trong phương trình hàm số f(x) = ax + b. Từ đó, ta có thể xác định được tính biến thiên của hàm số dựa vào các trường hợp sau:

• Nếu hệ số a = 0, tức là đường thẳng là một đường ngang, hàm số sẽ không thay đổi khi giá trị của biến số x thay đổi. Do đó, hàm số sẽ có tính chất biến thiên đồng nhất, không tăng cũng không giảm.
• Nếu hệ số a ≠ 0, hàm số sẽ thay đổi khi giá trị của biến số x thay đổi. Trường hợp này có hai trường hợp nhỏ hơn:
• Nếu hệ số a > 0, thì khi giá trị của biến số x tăng, giá trị của hàm số sẽ tăng theo giá trị của biến số x.
• Nếu hệ số a < 0, thì khi giá trị của biến số x tăng, giá trị của hàm số sẽ giảm theo giá trị của biến số x.

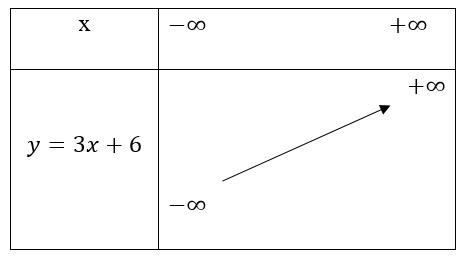
Ví dụ: Lập bảng biến thiên của các hàm số sau đây:

y = 3x + 6

TXĐ: R, ta có: a = 3 > 0

⇒ Hàm số đồng biến trên R. Ta có bảng biến thiên như sau:

Ứng dụng của Hàm số bậc nhất

• Giải các hệ phương trình tuyến tính: Hàm số bậc nhất được sử dụng để giải các hệ phương trình tuyến tính, trong đó có nhiều biến số và các phương trình có dạng tuyến tính.
• Xác định đường thẳng gần nhất: Hàm số bậc nhất có thể được sử dụng để xác định đường thẳng gần nhất đi qua một tập hợp các điểm cho trước.
• Tính toán tài chính: Trong lĩnh vực tài chính, hàm số bậc nhất được sử dụng để tính toán giá trị tương lai, giá trị hiện tại và tỷ suất sinh lời. Công thức cơ bản của các khái niệm này thường dựa trên hàm số bậc nhất.
• Vật lý và kỹ thuật: Trong lĩnh vực vật lý và kỹ thuật, hàm số bậc nhất được sử dụng để mô hình hóa quan hệ giữa các biến số vật lý, chẳng hạn như quãng đường di chuyển, thời gian và vận tốc.

Các dạng toán về Hàm số bậc nhất thường gặp

Dạng 1: Phương pháp xác định hàm số bậc nhất

Bài tập: Tìm điều kiện của tham số m để hàm số y = (m-1)x + m là hàm số bậc nhất.

Gợi ý lời giải:

y = (m - 1)x + m

⇔ y = (m - 1)x + m

⇔ m - 1 ≠ 0 ⇔ m ≠ 1.

Vậy với điều kiện mọi m ≠ 1 thì hàm số y = (m - 1)x + m là hàm số bậc nhất.

Dạng 2: Tìm m để hàm số bậc nhất đồng biến, nghịch biến

Phương pháp giải: Áp dụng tính chất đồng biến, nghịch biến của hàm số bậc nhất

• Nếu a > 0 ⇒ Hàm số đồng biến trên R
• Nếu a < 0 ⇒ Hàm số nghịch biến trên R

Bài tập: Tìm m để hàm số y = (m - 3)x + 7 nghịch biến trên tập R xác định.

Gợi ý lời giải:

Để hàm số y = (m - 3)x + 7 nghịch biến trên tập xác định R, ta có:

⇔ m - 3 < 0 ⇔ m < 3.

Vậy với mọi m < 3 thì hàm số y = (m - 3)x + 7 nghịch biến trên tập R xác định.

Bài tập tự ôn luyện

Bài tập 1: Cho các hàm số y = 2mx + m + 1 (1) và hàm số y = (m - 1)x + 3 (2)

a) Xác định m đề hàm số (1) đồng biến, hàm số (2) nghịch biến.

b) Xác định m để đồ thị hàm số (1) song song với đồ thị hàm số (2)

Gợi ý lời giải:

a) Muốn xác định m để hàm số (1) đồng biến và hàm số (2) nghịch biến, ta có:

- Hàm số (1) đồng biến: 2m > 0 → m > 0

- Hàm số (2) nghịch biến: m - 1 < 0 → m < 1

→ Để hàm số (1) đồng biến và hàm số (2) nghịch biến thì m thỏa: 0 < m < 1.

b) Muốn xác định m để đồ thị hàm số (1) song song với đồ thị hàm số (2), ta có:

⇔ 2m = m - 1 và m + 1 ≠ 3

⇔ m = -1 và m ≠ 2

⇔ m = -1

→ Vậy để đồ thị hàm số (1) song song với đồ thị hàm số (2) thì m = -1.

Bài tập 2:

Cho hàm số: y = (m - 2)x + m + 3 (1) và hàm số y = 3x - 3 + m (2).

1. Tìm m để (1) đi qua điểm H(1; 2)
2. Tìm m để (1) và (2) song song với nhau.

Gợi ý lời giải:

1. Để (1) có thể đi qua điểm H(1; 2) thì ta thay x = 1 và y = 2 vào (1), ta có:

⇔ 2 = (m - 2).1 + m + 3

⇔ 2 = m - 2 + m + 3

⇔ 2 = 2m + 1

⇔ m = ½

Vậy để (1) đi qua điểm H(1; 2) thì m = ½.

2. Để (1) và (2) song song với nhau thì ta có:

⇔ m - 2 = 3 và m + 3 ≠ -3 + m

→ m = 5

Vậy để (1) và (2) song song với nhau thì m = 5.

Kết luận

Qua bài viết trên, thayphu mong rằng các bạn học sinh đã nắm rõ các khái niệm về hàm số bậc nhất như định nghĩa, tính chất, ứng dụng và các dạng toán của nó. Đây là một khái niệm tuy cơ bản nhưng đóng vai trò vô cùng quan trọng trong chương trình toán lớp 9 và tuyển sinh vào 10. Vì vậy các bạn hãy ôn tập thật kỹ để nắm chắc và vận dụng tốt phần kiến thức này nhé.