Các tính chất hình thoi và điều thú vị xung quanh chúng

Tính chất của hình thoi là những đặc điểm đặc trưng và độc đáo mà hình thoi có. Có nghĩa là mỗi cạnh của hình thoi có cùng độ dài với cạnh.

Hình thoi không chỉ có hình dáng đặc trưng với các cạnh bằng nhau, các góc vuông mà còn có những đặc tính đặc biệt và hấp dẫn. Trong bài viết này của thayphu chúng ta sẽ đi sâu vào những tính chất này để hiểu rõ hơn về hình thoi và tầm quan trọng của nó trong lĩnh vực hình học.

Định nghĩa về một hình thoi

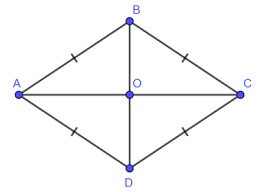
Định nghĩa về một hình thoi

Hình thoi là một hình hình học hai chiều có bốn cạnh có độ dài bằng nhau và các góc kề nhau là góc vuông. Đặc điểm đặc trưng của hình thoi là hai đường chéo cắt nhau vuông góc, chia hình thoi thành hai hình tam giác đều. Đường chéo lớn của hình thoi là đường nối hai đỉnh không kề nhau và có độ dài bằng đường chéo nhỏ. Hình thoi cũng có ít nhất hai đường đối xứng là .

Điều này có nghĩa là nếu bạn vẽ một đường thẳng đi qua trung điểm của hai cạnh kề thì hình thoi sẽ được sao chép dọc theo đường thẳng đó. Hình thoi là một dạng hình vuông đặc biệt trong đó tất cả các góc đều là góc vuông.

Cách chứng minh hình thoi

Để chứng minh một hình là hình thoi,bạn có thể sử dụng một trong các phương pháp sau:

Sử dụng định nghĩa

Chứng minh rằng hình đó thỏa mãn đầy đủ tính chất, đặc điểm của hình thoi gồm các cạnh bằng nhau, góc vuông và đường chéo cắt nhau trong các góc vuông và đối xứng. Nếu bạn có thể chứng minh được tất cả những đặc tính này thì đó chính là kim cương.

Sử dụng độ dài cạnh và góc

Đo độ dài các cạnh và góc của hình đó.Nếu tất cả các cạnh có cùng độ dài và tất cả các góc đều đúng thì đó là hình thoi.

Dùng đường chéo

Đo độ dài hai đường chéo của hình đó. Nếu hai đường chéo cắt nhau vuông góc và có cùng độ dài thì đó là hình thoi.

Sử dụng phép đối xứng

Vẽ đường thẳng đi qua trung điểm của hai cạnh kề nhau.Nếu hình thoi được sao chép dọc theo đường này và tạo ra sự đối xứng hoàn hảo thì đó là hình thoi.

Sử dụng công thức tính diện tích và chu vi

Tính diện tích và chu vi của một hình. Nếu phép tính cho diện tích tương ứng với công thức (S = (d1 * d2)/2) và chu vi tương ứng với công thức (P = 4a),trong đó d1 và d2 là độ dài của hai đường chéo và a là chiều dài của bên cạnh thì đó là một hình thoi.Với bất kỳ phương pháp nào, điều quan trọng là phải cẩn thận và chính xác trong các phép đo, tính toán để đảm bảo kết quả chính xác.

Các cạnh của hình thoi có bằng nhau không?

Nếu các cạnh của một hình không bằng nhau thì hình đó không phải là hình thoi. Một trong những đặc điểm chính của hình thoi là các cạnh của nó có cùng chiều dài. Nếu các cạnh không bằng nhau thì hình đó có thể là hình chữ nhật, hình bình hành hoặc đa giác khác nhưng không phải là hình thoi. Để xác định xem một hình có phải là hình thoi hay không, bạn cần kiểm tra các thuộc tính cạnh bằng nhau và các đặc điểm khác của hình thoi, chẳng hạn như:

góc vuông và đường chéo cắt nhau ở góc vuông.

Cách tính các đường chéo của hình thoi

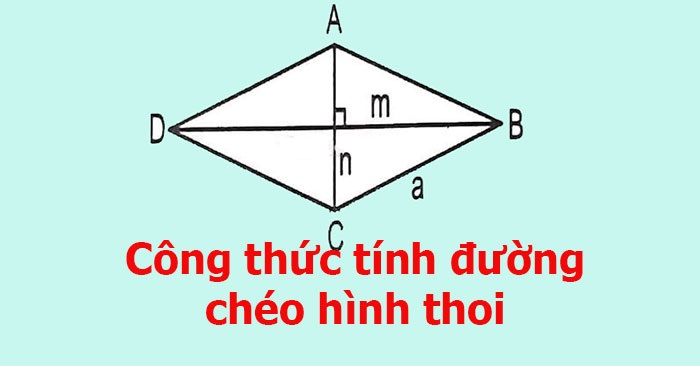
Cách tính các đường chéo của hình thoi

Để tính độ dài đường chéo của hình thoi, bạn có thể sử dụng các công thức và phép tính dựa trên thông tin đã biết về hình thoi.

Gọi độ dài một cạnh của hình thoi là.

Đường chéo chính (đường chéo lớn)

Đường chéo chính chia hình thoi thành hai tam giác vuông cân. Độ dài của đường chéo chính có thể được tính bằng định lý Pythagore, trong đó đường chéo chính là cạnh huyền của hai tam giác vuông cân.Đường chéo chính = a * √2

Đường chéo phụ (đường chéo nhỏ)

Đường chéo phụ là đoạn thẳng nối hai đỉnh không kề nhau của hình thoi. Để tính độ dài của đường chéo phụ,bạn có thể sử dụng các định lý và quy tắc hình thoi.

Đường chéo nhỏ = a

Sử dụng công thức trên, bạn có thể tính độ dài cả hai đường chéo của hình thoi từ độ dài một cạnh của hình thoi.

Bài tập áp dụng

Bài tập 1:Cho một hình thoi ABCD với đường chéo chính AC. Chứng minh rằng đường thẳng AB song song với đường thẳng DC.

Đáp án:

Ta có:

Góc ACD = Góc ABD (cùng là góc nhọn)

Góc ACD = Góc ADC (góc vuông)

Vậy, góc ABD = góc ADC.

Do đó, AB // DC (đường thẳng AB song song với đường thẳng DC).

Bài tập 2:

Cho một hình thoi ABCD với đường chéo chính AC. Chứng minh rằng đường chéo BD là trục đối xứng của đường chéo AC.

Đáp án:

Ta có:

Góc ABD = Góc DBC (cùng là góc nhọn)

Góc ABD = Góc BDA (góc vuông)

Vậy, góc DBC = góc BDA.

Do đó, BD là trục đối xứng của AC.

Bài tập 3:

Cho một hình thoi ABCD với đường chéo chính AC. Chứng minh rằng tứ giác ABCD là hình bình hành.

Đáp án:

Ta có:

AB = CD (hai cạnh đối nhau của hình thoi)

AD = BC (hai cạnh đối nhau của hình thoi)

Góc DAB = Góc BCD (cùng là góc nhọn)

Góc ABD = Góc DCA (cùng là góc nhọn)

Vậy, tứ giác ABCD là hình bình hành.

Bài tập 4:

Cho một hình thoi ABCD với đường chéo chính AC. Chứng minh rằng đường cao của tam giác ABC đi qua điểm giao của đường chéo BD.

Đáp án:

Gọi H là giao điểm của đường cao từ A của tam giác ABC và đường chéo BD.

Ta cần chứng minh H thuộc đường chéo AC.

Chứng minh:

Góc AHB = Góc ABD (cùng là góc nhọn)

Góc AHB = Góc ABC (góc vuông)

Vậy, góc ABD = góc ABC.

Do đó, tam giác ABD đồng dạng với tam giác ABC.

Vì vậy, tỉ số cạnh đối của hai tam giác là bằng nhau:

AB / AD = BC / AB

AB^2 = BC * AD

Vì AB = BC (hai cạnh đối nhau của hình thoi), ta có:

AB^2 = AB * AD

AB = AD

Vậy, H thuộc đường chéo AC.

Bài tập 5:

Cho một hình thoi ABCD với đường chéo chính AC. Chứng minh rằng tứ giác ABDC là hình chữ nhật.

Đáp án:

Ta có:

Đường chéo AC chia tứ giác ABCD thành hai tam giác vuông cân.

Góc ABC = Góc ADC (góc vuông)

Góc BAC = Góc CAD (góc nhọn)

Do đó, tứ giác ABDC là hình chữ nhật.

Bài tập 6:

Cho một hình thoi ABCD với đường chéo chính AC. Chứng minh rằng tứ giác ABDC là tứ giác điều hòa.

Đáp án:

Ta cần chứng minh rằng tỉ số hai cặp cạnh đối của tứ giác ABDC bằng nhau.

Gọi E là giao điểm của đường chéo AC và BD.

Chứng minh:

Góc ABE = Góc DCE (cùng là góc nhọn)

Góc ABE = Góc ADE (góc vuông)

Vậy, góc DCE = góc ADE.

Do đó, tam giác DCE đồng dạng với tam giác ADE.

Vì vậy, tỉ số cạnh đối của hai tam giác là bằng nhau:

AD / AC = DE / CE

Đồng thời, góc BAC = góc ECD (cùng là góc nhọn)

Vậy, tỉ số cạnh đối của hai tam giác là bằng nhau:

AB / AC = BE / CE

Từ đó suy ra:

AD / AC = AB / AC

AD = AB

Vậy, tứ giác ABDC là tứ giác đều

Bài tập 7:

Cho một hình thoi ABCD với đường chéo chính AC. Chứng minh rằng đường phân giác góc BAC cắt đường chéo BD tại một điểm nằm trên đường cao từ D của tam giác ABD.

Đáp án:

Gọi E là giao điểm của đường phân giác góc BAC và đường chéo BD.

Ta cần chứng minh rằng E thuộc đường cao từ D của tam giác ABD.

Chứng minh:

Góc BAD = Góc BDA (cùng là góc nhọn)

Góc BAD = Góc DAB (góc vuông)

Vậy, góc BDA = góc DAB.

Do đó, tam giác ABD đồng dạng với tam giác DBA.

Vì vậy, tỉ số cạnh đối của hai tam giác là bằng nhau:

AB / AD = BD / AB

AB^2 = AD * BD

Vì AB = AD (hai cạnh đối nhau của hình thoi), ta có:

AB^2 = AB * BD

AB = BD

Vậy, E thuộc đường cao từ D của tam giác ABD.

Bài tập 8:

Cho một hình thoi ABCD với đường chéo chính AC. Chứng minh rằng đường phân giác góc ADB cắt đường cao từ C của tam giác CBD tại một điểm nằm trên đường chéo AC.

Đáp án:

Gọi F là giao điểm của đường phân giác góc ADB và đường cao từ C của tam giác CBD.

Ta cần chứng minh rằng F thuộc đường chéo AC.

Chứng minh:

Góc BCF = Góc ABD (cùng là góc nhọn)

Góc BCF = Góc CBD (góc vuông)

Vậy, góc ABD = góc CBD.

Do đó, tam giác ABD đồng dạng với tam giác CBD.

Vì vậy, tỉ số cạnh đối của hai tam giác là bằng nhau:

AD / AB = BC / CD

Vì AB = CD (hai cạnh đối nhau của hình thoi), ta có:

AD / AB = BC / AB

AD = BC

Vậy, F thuộc đường chéo AC.

Thayphu.net hy vọng những bài tập này đã giúp bạn nắm vững kiến thức về hình thoi và rèn luyện kỹ năng giải quyết vấn đề trong lĩnh vực này.