Cách tính thể tích khối hộp chữ nhật và bài tập áp dụng

Khối hộp chữ nhật là một dạng hình học cơ bản và quan trọng trong hình học không gian, tính chất, các cách tính thể tích và ứng dụng của khối hình hộp chữ nhật.

Thể tích khối hộp chữ nhật là một trong những dạng toán cơ bản, quan trọng trong hình học không gian, đặc biệt là trong chương trình Toán THPT và thường xuyên hiện trong các đề thi. Vì vậy, trong bài viết này, thayphu sẽ cùng các bạn tìm hiểu về khái niệm, tính chất, các cách tính thể tích khối hộp chữ nhật và ứng dụng của nó trong thực tế. Ngoài ra, còn có bài tập vận dụng về dạng toán này để các bạn học sinh có thể ôn tập, củng cố để nắm vững dạng toán này.

Hình hộp chữ nhật là gì?

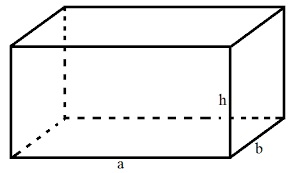
Hình hộp chữ nhật là một hình hộp có 6 mặt đều là hình chữ nhật, trong đó có 2 mặt không có cạnh chung được gọi là mặt đáy hay là hai mặt đối diện, còn các mặt còn lại được gọi là mặt bên.

Tính chất của hình hộp chữ nhật

• Hình hộp chữ nhật có 6 mặt, 8 đỉnh và 12 cạnh.
• Hai đường chéo của hình hộp chữ nhật có cùng độ dài và cắt nhau tại trung điểm của chúng.
• Diện tích của mỗi mặt có thể được tính bằng cách nhân độ dài hai cạnh đối diện của mặt đó.
• Diện tích của hai mặt đối diện trong hình hộp chữ nhật bằng nhau, tức là diện tích của mặt đáy và mặt đối diện với mặt đáy bằng nhau.
• Hình hộp chữ nhật có các trục đối xứng là các đường trung trực của các cạnh đối diện.

Các cách tính thể tích của khối hộp chữ nhật

Cách 1: cách tính thể tích bằng công thức tổng quát

V = a x b x h

Trong đó:

• V được kí hiệu là thể tích hình hộp chữ nhật.
• a là chiều dài hình hộp
• b là chiều rộng hình hộp
• h là chiều cao hình hộp

Cách 2: Tính tổng diện tích của ba mặt bên và cạnh bằng nhau

V = 2(ab + ac + bc)

Trong đó a, b,c lần lượt là chiều dài, chiều rộng và chiều cao của khối hộp chữ nhật.

Ví dụ: Cho một hộp chữ nhật có chiều dài a = 10 cm, chiều rộng b = 5 cm và chiều cao c = 6 cm.

Ta có thể tính thể tích bằng cách tính tổng diện tích các mặt bên và cạnh bằng nhau.

V = 2(ab + ac + bc) = 2(10x5 + 10x6 + 5x6) = 280 cm^3

Cách 3: Tính thể tích khi biết chu vi của khối hộp chữ nhật

Nếu đề bài chỉ cho ta biết được chu vi (C) của khối hình hộp chữ nhật, và 2 trên 3 cạnh của hình hộp chữ nhật. Ta có thể suy ra cạnh còn lại để có đầy đủ dữ kiện giải bài toán.

Chu vi C được tính bằng công thức: C = 4a + 4b + 4c.

Sau khi đã tất cả các cạnh của hình hộp, áp dụng công thức tổng quát như đã cho ở trên để tính thể tích khối hộp.

Ứng dụng của khối hộp chữ nhật trong thực tế

• Xây dựng và kiến trúc: Trong ngành xây dựng, tính toán thể tích khối hộp chữ nhật là rất quan trọng để ước lượng lượng vật liệu cần thiết, như bê tông, gạch, sơn, hay các vật liệu xây dựng khác. Từ đó, ta có thể đảm bảo tính chính xác và hiệu quả trong quá trình xây dựng.
• Lưu trữ và vận chuyển: Thể tích khối hộp chữ nhật cũng được sử dụng để tính toán dung tích và khối lượng của các đồ vật trước khi lưu trữ hoặc vận chuyển chúng. Ví dụ, trong ngành vận tải và logistics, việc biết được thể tích khối hộp chữ nhật của một đơn vị hàng hóa giúp quản lý kho và lập kế hoạch vận chuyển một cách hiệu quả.
• Thiết kế sản phẩm: Trong thiết kế sản phẩm, kiến thức về thể tích khối hộp chữ nhật giúp xác định không chỉ kích thước mà còn tính toán được dung tích của sản phẩm. Giúp cho việc thiết kế sản phẩm có khả năng đáp ứng yêu cầu của khách hàng và cung cấp thông tin quan trọng cho quy trình sản xuất.
• Giáo dục: Khái niệm về thể tích khối hộp chữ nhật cũng được giảng dạy trong chương trình toán hình học không gian ở THPT. Nó giúp học sinh hiểu về mối liên hệ giữa các đại lượng hình học và áp dụng chúng vào các bài toán thực tế. Đây được coi là dạng toán quan trọng cần nắm rõ để làm nền tảng cho các dạng toán nâng cao.

Kết luận

Qua bài viết trên, chắc hẳn các bạn học sinh cũng đã hiểu được định nghĩa, tính chất, ứng dụng, và đặc biệt là các cách tính thể tích của khối hộp chữ nhật để áp dụng chúng vào các dạng toán khác nhau. Mong rằng các bạn đã nắm rõ được dạng toán này và áp dụng thật tốt vào quá trình giải đề. Bởi lẽ đây là nền tảng rất quan trọng để xây dựng nên những bài toán nâng cao và phức tạp hơn.Từ đó đưa chúng ra áp dụng ngoài thực tế như kiến trúc, đồ họa đến lĩnh vực kỹ thuật và xây dựng.