Quy tắc và cách nhận biết phương trình chứa dấu giá trị tuyệt đối

Phương trình chứa dấu giá trị tuyệt đối là một loại phương trình trong đó có sự tham gia của hàm giá trị tuyệt đối và được kí hiệu bằng dấu.

Chúng xuất hiện khi chúng ta cần tìm giá trị của các biến thỏa mãn một điều kiện nhất định, không phân biệt số dương hay số âm. Trong bài viết này thayphu sẽ tìm hiểu cách giải và áp dụng nó

Định nghĩa về phương trình chứa dấu giá trị tuyệt đối

Định nghĩa

Chúng là loại phương trình chứa hàm giá trị tuyệt đối. Các hàm giá trị tuyệt đối, thường được kí hiệu bằng dấu | xung quanh biểu thức, và trả về giá trị tuyệt đối của biểu thức đó.

Khi áp dụng vào một phương trình, nó tạo ra các điều kiện xảy ra cho cả giá trị dương và giá trị âm của biến.

Ký hiệu của phương trình chứa dấu giá trị tuyệt đối

Phương trình có ký hiệu giá trị tuyệt đối thường có dạng f(x) = g(x), trong đó f(x) và g(x) là các biểu thức chứa biến x và f(x) biểu thị giá trị tuyệt đối của f(x).

Phương trình này có nghĩa là ta tìm các giá trị của x sao cho khi thay f(x) thì giá trị tuyệt đối của f(x) bằng giá trị của g(x).

Để giải phương trình chứa

giá trị tuyệt đối, chúng ta thường phải xét các tình huống có thể xảy ra.

Điều này là do phương trình có thể có nhiều nghiệm, bao gồm giá trị dương và âm của các biến.

Điều quan trọng là phải kiểm tra từng trường hợp để xác định các giá trị thỏa mãn phương trình.

Chúng có nhiều ứng dụng thực tế, ví dụ như trong các bài toán về khoảng cách, giá trị tuyệt đối, so sánh và tối ưu hóa. Việc hiểu và áp dụng được phương trình này sẽ giúp chúng ta giải được một số bài toán có tính ứng dụng cao.

Dấu hiệu nhận biết phương trình chứa dấu giá trị tuyệt đối

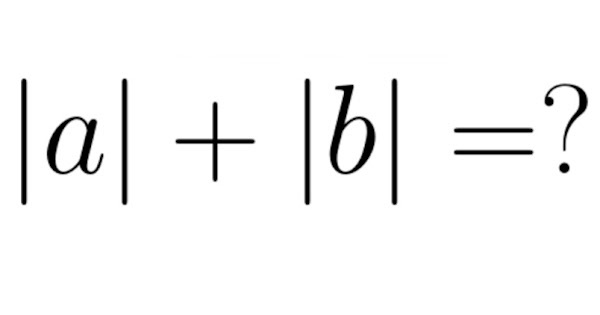
Dấu hiệu nhận biết

Có một số dấu hiệu giúp chúng ta nhận biết phương trình có chứa ký hiệu giá trị tuyệt đối.

Dưới đây là một số dấu hiệu chúng ta thường gặp:

• Sự xuất hiện của dấu | xung quanh biểu thức: Các phương trình chứa ký hiệu giá trị tuyệt đối thường được đánh dấu bằng dấu | xung quanh biểu thức.Ví dụ: f(x) = g(x).
• So sánh giữa hai biểu thức: Trong các phương trình chứa ký hiệu giá trị tuyệt đối, chúng ta thường thấy sự so sánh giữa hai biểu thức.Ví dụ: x + 3 = 5.
• Sự tham gia của hàm giá trị tuyệt đối: Phương trình có dấu giá trị tuyệt đối thường có hàm giá trị tuyệt đối, được ký hiệu là f(x). Điều này cho thấy rằng chúng ta cần quan tâm đến giá trị tuyệt đối của biểu thức f(x).
• Sự xuất hiện của các giá trị tuyệt đối trong bài toán: Nếu bài toán yêu cầu tìm các giá trị thỏa mãn điều kiện bất kể chiều dương hay chiều âm thì rất có thể phương trình chứa dấu trong giá trị tuyệt đối.

Các quy tắc dấu khi tìm phương trình chứa dấu giá trị tuyệt đối

Khi tìm phương trình chứa dấu giá trị tuyệt đối, chúng ta cần áp dụng quy tắc dấu phù hợp để giải quyết các trường hợp khác nhau. Dưới đây là quy tắc dấu cơ bản:

Trường hợp dấu dương

Khi giá trị trong dấu giá trị tuyệt đối là dương (|x| > 0), ta có:

|f(x)| = g(x) tương đương với f(x) = g(x).

Trường hợp dấu âm

Khi giá trị trong dấu giá trị tuyệt đối là âm (|x| < 0), ta có:

|f(x)| = g(x) tương đương với f(x) = -g(x).

Trường hợp hai dấu

Khi giá trị trong dấu giá trị tuyệt đối có thể là dương hoặc âm (|x| ≥ 0), ta cần chia phương trình thành hai trường hợp riêng biệt:

• Khi f(x) ≥ 0 (dấu dương):
• |f(x)| = g(x) tương đương với f(x) = g(x).
• Khi f(x) < 0 (dấu âm):
• f(x)| = g(x) tương đương với f(x) = -g(x).

Một số dạng toán giải phương trình chứa dấu giá trị tuyệt đối

Dưới đây là một số dạng toán giải phương trình mà chúng ta thường gặp:

Dạng 1: Phương trình tiếp tuyến chứa dấu giá trị tuyệt đối

|ax + b| = c, trong đó a, b, và c là các hằng số đã biết.

Ví dụ: |2x - 3| = 7.

Cách giải :

Trường hợp 1: ax + b = c

Giải phương trình tiếp tuyến bình thường: 2x - 3 = 7

=> x = 5

Trường hợp 2: - (ax + b) = c

Đảo dấu và giải phương trình tiếp tuyến: -(2x - 3) = 7

=> -2x + 3 = 7

=> -2x = 4

=> x = -2

Phương trình có hai đáp số: x = 5 và x = -2.

Dạng 2:Phương trình bậc hai chứa dấu giá trị tuyệt đối

|ax^2 + bx + c| = d, trong đó a, b, c, và d là các hằng số đã biết và a khác 0.

Ví dụ: |x^2 - 4x - 5| = 9.

Cách giải :

Trường hợp 1: ax^2 + bx + c = d

Giải phương trình bậc hai bình thường: x^2 - 4x - 5 = 9

=> x^2 - 4x - 14 = 0

=> (x - 7)(x + 2) = 0

=> x = 7 hoặc x = -2

Trường hợp 2: - (ax^2 + bx + c) = d

Đảo dấu và giải phương trình bậc hai: -(x^2 - 4x - 5) = 9

=> -x^2 + 4x + 5 = 9

=> -x^2 + 4x - 4 = 0

=> x^2 - 4x + 4 = 0

=> (x - 2)^2 = 0

=> x = 2

Phương trình có ba đáp số: x = 7, x = -2, và x = 2.

Dạng 3:Phương trình vô tỉ chứa dấu giá trị tuyệt đối

|a/x + b| = c, trong đó a, b, và c là các hằng số đã biết và x là biến số.

Ví dụ: |3/x + 2| = 4.

Cách giải:

Trường hợp 1: a/x + b = c

Giải phương trình tiếp tuyến: 3/x + 2 = 4

=> 3/x = 2

=> x/3 = 1/2

=> x = 3/2

Trường hợp 2: - (a/x + b) = c

Đảo dấu và giải phương trình tiếp tuyến: -(3/x + 2) = 4

=> -3/x - 2 = 4

=> -3/x = 6

=> x/3 = -1/6

=> x = -½

Phương trình có hai đáp số: x = 3/2 và x = -1/2.

Một số lưu ý khi giải hương trình chứa dấu giá trị tuyệt đối

Khi giải các phương trình , sau đây là một số lưu ý quan trọng:

• Chia các trường hợp: Phương trình chứa ký hiệu tuyệt đối thường có nhiều nghiệm, trong đó có giá trị dương và giá trị âm của các biến. Vì vậy, điều quan trọng là phải chia phương trình thành từng trường hợp riêng biệt tùy theo giá trị của biểu thức ở giá trị tuyệt đối.
• Xác định giá trị dương, giá trị âm: Để áp dụng quy tắc dấu cần xác định giá trị dương, giá trị âm của biểu thức trong dấu của giá trị tuyệt đối.Điều này giúp xác định các trường hợp cần giải quyết và áp dụng các quy tắc đánh giá phù hợp.
• Sử dụng bất đẳng thức: Trong một số trường hợp, việc sử dụng bất đẳng thức có thể hữu ích để giải các phương trình chứa ký hiệu giá trị tuyệt đối. Bằng cách áp dụng quy tắc bất đẳng thức, bạn có thể xác định giới hạn giá trị của biến và tìm ra nghiệm tương ứng.
• Xác minh giá trị: Sau khi tìm nghiệm cho từng trường hợp, điều quan trọng là phải xác minh phương trình ban đầu để xem giá trị tìm được có thỏa mãn điều kiện ban đầu hay không.

Bài tập áp dụng

• Bài 1:Tìm giá trị của x thỏa mãn phương trình |2x - 3| = 5.

a) x = -1

b) x = 2

c) x = 4

d) x = 5

Đáp án: b) x = 2

• Bài 2:Phương trình |x - 4| - 2 = 3 có bao nhiêu nghiệm?

a) 0

b) 1

c) Vô số nghiệm

Đáp án: a) 0

• Bài 3:Tìm tất cả các giá trị của x thỏa mãn phương trình |x + 2| = |x - 2|.

a) x = -2

b) x = 0

c) x = 2

d) Tất cả các giá trị trên

Đáp án: d) Tất cả các giá trị trên

• Bài 4:Phương trình |x - 1| + |x - 3| = 4 có bao nhiêu nghiệm?

a) 0

b) 1

c) 2

d) Vô số nghiệm

Đáp án: c) 2

• Bài 5:Tìm tất cả các giá trị của x thỏa mãn phương trình |x^2 - 9| = 0.

a) x = -3, x = 3

b) x = -3, x = 3, x = 0

c) x = 0

d) Không có nghiệm

Đáp án: a) x = -3, x = 3

Kết luận

Mong rằng các bài tập đã giúp các bạn ôn tập và nắm vững kiến thức về phương trình có ký hiệu tuyệt đối. Phương trình này là một khái niệm quan trọng trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực. Bằng cách thực hành các bài tập giải, bạn sẽ nắm vững cách tiếp cận và tìm ra giải pháp cho các phương trình này.