Phương trình bậc nhất 1 ẩn, định nghĩa, cách giải và bài tập

Phương pháp giải phương trình bậc nhất một ẩn. Định nghĩa, quy tắc, các dạng toán thường gặp của phương trình bậc nhất 1 ẩn.

Trong chương trình toán học lớp 8, các bạn học sinh sẽ được làm quen với các kiến thức mới về phương trình. Và phần kiến thức cơ bản nhất chính là kiến thức về phương trình bậc nhất 1 ẩn. Đây được coi là một khái niệm quan trọng trong toán học lớp 8.

Vì vậy trong bài viết này, các bạn hãy cùng thayphu tìm hiểu về công thức cơ bản, các quy tắc, phương pháp giải và các dạng bài tập cơ bản thường gặp của phương trình bậc nhất, ngoài ra còn cung cấp ví dụ minh họa để học sinh lớp 8 có thể áp dụng kiến thức này một cách dễ dàng.

Định nghĩa phương trình bậc nhất

Phương trình bậc nhất 1 ẩn là một loại phương trình toán học có dạng ax + b = 0. Trong đó a và b là các hệ số cố định và x là ẩn, a khác 0 vì nếu a = 0, phương trình sẽ không còn là phương trình bậc nhất nữa.

Ví dụ:

2x - 3 = 0

5x + 13 = 0

Quy tắc để biến đổi một phương trình bậc nhất

Quy tắc chuyển vế các số hạng

Khi ta chuyển một số hạng từ một vế sang vế khác của bất phương trình, ta luôn phải đổi dấu của số đó. Ví dụ, nếu ta chuyển +b sang vế khác, nó sẽ trở thành -b.

Ví dụ: Giải bất phương trình sau: x + 3 < 0

⇔ x < - 3 ( 3 đổi sang vế khác thì đổi dấu thành -3).

Quy tắc nhân với một số

Khi nhân cả hai vế với một số khác không, tính đẳng thức của phương trình được giữ nguyên và nghiệm của phương trình sau khi nhân có thể thay đổi.

Ví dụ: Giải phương trình sau: x/7 = 7

⇔ (x/7).7 = 7.7

⇔ x = 49 (nhân cả 2 vế với 7 ta được x = 49)

Phương pháp giải phương trình bậc nhất một ẩn

Phương trình có dạng ax + b = 0 (với a ≠ 0)

• Bước 1: Xác định giá trị của a và b trong phương trình ax + b = 0.
• Bước 2: Nếu a ≠ 0, ta chia cả hai vế của phương trình cho a để tìm giá trị của x. Phương trình trở thành x = -b/a.
• Bước 3: Tính x và kết luận (nếu x là số nguyên) hoặc tính giá trị của x bằng cách thay giá trị của a và b vào biểu thức x = -b/a.

Ví dụ: Giải phương trình 2x - 4 = 0.

• Bước 1: a = 2 và b = -4
• Bước 2: Chia cả hai vế của phương trình cho a: (2x - 4)/2 = 0/2, hoặc x - 2 = 0
• Bước 3: Giá trị của x là 2

Vậy, giá trị của x trong phương trình 2x - 4 = 0 là x = 2.

Các dạng toán thường gặp

Dạng 1: Đưa về dạng phương trình bậc nhất

• Chuyển các hạng tử có chứa ẩn sang cùng 1 vế và các hằng số sang vế khác.
• Thu gọn phương trình về dạng cơ bản là ax + b = 0.
• Giải phương trình và kết luận.

Ví dụ: 4x - 9 = 12x + 3

⇔ 12x - 4x = -9 -3

⇔ 8x = -12

→ x = -12/8 = -3/2

Vậy x = -3/2

Dạng 2: Giải dạng phương trình tích

Phương trình tích là phương trình có dạng: A(x).B(x) = 0

Để giải quyết dạng toán về phương trình tích như trên, ta có:

A(x).B(x) = 0 ⇔ A(x) = 0 hoặc B(x) = 0

Giải hai phương trình A(x) = 0 hoặc B(x) = 0 và nhận tất cả các nghiệm của 2 phương trình.

Ví dụ: (7x - 14).(5x - 2) = 0

⇔ 7x - 14 = 0 hoặc 5x - 2 = 0

⇔ 7x = 14 hoặc 5x = 2

⇔ x = 2 hoặc x = ⅖

→ Vậy phương trình trên có tập nghiệm là S = {2; ⅖}.

Dạng 3: Giải phương trình có ẩn ở mẫu

Phương trình có ẩn ở mẫu có dạng là

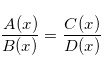
Để giải quyết dạng toán về phương trình có ẩn ở mẫu như trên, ta thực hiện các bước như sau:

• Bước 1: Tìm điều kiện xác định và đặt ẩn cho phương trình đã cho.
• Bước 2: Biểu diễn các đại lượng chưa biết theo ẩn đã đặt hoặc theo các đại lượng đã biết.
• Bước 3: Lập và giải phương trình, so kết quả với ĐKXĐ rồi kết luận.

Ví dụ: Tìm 2 số nguyên liên tiếp, biết rằng hai lần số nhỏ cộng ba lần số lớn bằng 13.

Gọi số nguyên có giá trị nhỏ hơn là x, vậy suy ra số nguyên lớn hơn là x + 1.

Ta có phương trình theo đề bài yêu cầu như sau:

2x + 3(x + 1) = 13

⇔ 2x + 3x + 3 = 13

⇔ 5x = 10

⇔ x = 2

Vậy số nguyên nhỏ là 2, số nguyên lớn là 3.

Kết luận

Qua bài viết này, thayphu hy vọng các bạn học sinh có thể nắm rõ khái niệm phương trình bậc nhất 1 ẩn, hiểu được chi tiết các quy tắc, phương pháp giải và các dạng toán thường gặp của khái niệm này. Bởi lẽ, phương trình bậc nhất thường được sử dụng trong nhiều bài toán thực tế, ví dụ như tính toán trong kinh tế, vật lý, hóa học, và trong cuộc sống hàng ngày. Đây là 1 khái niệm cơ bản nhưng quan trọng trong toán học và đời sống. Vì vậy, các bạn hãy học và ôn luyện thật kỹ các ví dụ và dạng bài tập khác nhau để nắm rõ và thành thạo nó. Từ đó xây dựng nền tảng để giải các dạng nâng cao hơn nữa.