Phép chia phân thức đại số, ứng dụng và tổng hợp dạng toán

Khái niệm về phép chia phân thức đại số, cách thực hiện phép chia, các ví dụ minh họa chi tiết và các dạng toán từ cơ bản đến nâng cao của phép chia phân thức.

Phép chia phân thức đại số là một khái niệm cơ bản và quan trọng trong đại số đặc biệt là trong chương trình toán lớp 8. Phép chia phân thức là quá trình chia một phân thức này cho một phân thức khác, giúp chúng ta rút gọn biểu thức và tính ra giá trị chính xác của phân thức đó.

Trong bài viết này, hãy cùng thayphu tìm hiểu về phép chia phân thức, cách thực hiện phép chia và một số ví dụ minh họa cụ thể để giúp các bạn học sinh hiểu rõ hơn về khái niệm này nhé.

Kiến thức về phân thức và phép chia phân thức đại số

Phân thức nghịch đảo

Định nghĩa: Nếu tích của hai phân số bằng 1 thì chúng được gọi là hai phân thức nghịch đảo.

Công thức:

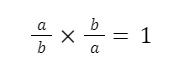
Từ đó suy ra, phân thức nghịch đảo của a/b là b/a.

Ví dụ: Hãy tìm phân thức nghịch đảo của các phân số sau đây:

2x, (x - 3) / (x + 5)

• Phân thức nghịch đảo của 2x là 1/2x
• Phân thức nghịch đảo của (x - 3) / (x + 5) là (x + 5) / (x - 3)

Phép chia phân thức đại số

Định nghĩa: Để chia phân thức a/b cho một phân thức c/d khác 0, ta phải nhân a/b với nghịch đảo của c/d.

Công thức:

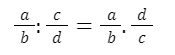
Với c/d khác 0.

Ví dụ: Chia hai phân thức sau đây:

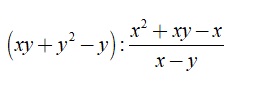
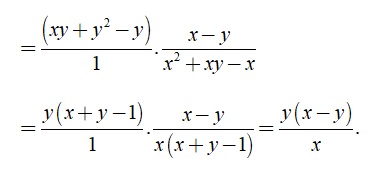
Các dạng toán về phép chia phân thức thường gặp

Dạng 1: Áp dụng quy tắc chia để thực hiện phép tính

Phương pháp: Sử dụng công thức đã cho ở phần lý thuyết.

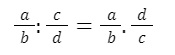
Lưu ý:

• Đối với phép chia có nhiều hơn hai phân số, ta nhân với nghịch đảo của các phân số sau dấu chia theo thứ tự từ trái qua phải.
• Ưu tiên tính toán trước các biểu thức trong ngoặc đơn (nếu có)

Bài tập: Thực hiện phép tính chia các phân thức đại số sau đây

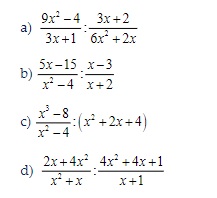
Gợi ý lời giải:

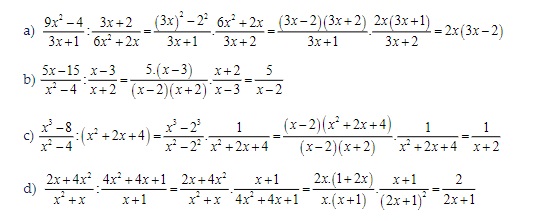
Dạng 2: Tính giá trị phân thức thỏa mãn đẳng thức đã cho

Phương pháp: Thực hiện theo hai bước sau:

• Bước 1. Đặt phân số cần tìm sang một vế riêng.
• Bước 2. Áp dụng quy tắc nhân và chia các phân thức để tính ra phân số cần tìm.

Bài tập: Tìm phân thức C thỏa mãn biểu thức sau đây:

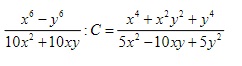
Gợi ý lời giải:

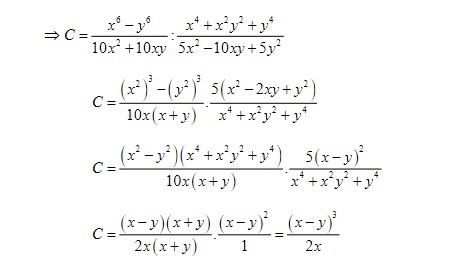
Dạng 3: Các dạng toán nâng cao

Bài tập: Cho phân thức như sau:

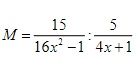
Tính giá trị của ẩn x để giá trị của phân thức M đã cho là một biểu thức có giá trị nguyên.

Gợi ý lời giải:

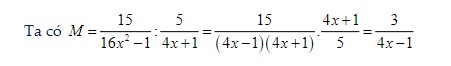
Để giá trị của phân thức M đã cho là một biểu thức có giá trị nguyên thì

3 ⋮ (4x - 1) → 4x - 1 ∈ Ư (3)

→ 4x - 1 ∈ {-3; -1; 1; 3} → x ∈ {-½; 0; ½; 1}

Vậy x ∈ {-½; 0; ½; 1} thì giá trị của M là một biểu thức mang giá trị nguyên.

Các ứng dụng của phép chia phân thức trong toán học

• Rút gọn biểu thức đại số: Phép chia phân thức được sử dụng để rút gọn biểu thức đại số. Bằng cách thực hiện phép chia phân thức và rút gọn kết quả, chúng ta có thể đơn giản hóa biểu thức và dễ dàng tính toán và tìm ra lời giải cho bài toán.
• Giải phương trình: Phép chia phân thức cũng được sử dụng để giải các phương trình đại số. Khi giải phương trình, ta có thể áp dụng phép chia phân thức để rút gọn biểu thức và tìm giá trị của biến.
• Tìm giá trị hàm số:Trong một số trường hợp, chúng được sử dụng để tính giá trị của hàm số. Ta có thể tìm giá trị của hàm số tại 1 điểm bằng cách chia phân thức biểu diễn hàm số cho một giá trị cụ thể của biến.
• Tính đạo hàm: Khi tính đạo hàm, ta thường phải thực hiện các phép chia phân thức để rút gọn biểu thức và tính toán đạo hàm.
• Quy tắc nhân và chia trong đại số:Phép chia phân thức là một trong những quy tắc cơ bản trong đại số. Nắm vững phép chia phân thức là kỹ năng quan trọng để áp dụng các quy tắc nhân và chia trong đại số, và tính đúng giá trị của biểu thức đại số.

Bài tập tự ôn luyện

Bài tập 1: Làm phép tính chia các phân thức sau:

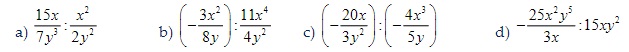
Gợi ý lời giải:

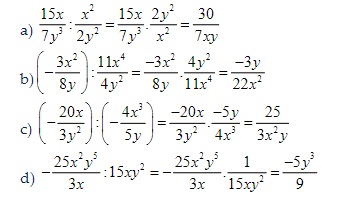
Bài tập 2: Tìm Q, biết:

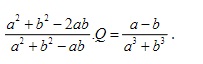
Gợi ý lời giải:

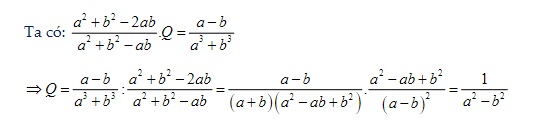
Bài tập 3: Rút gọn các phân thức sau:

Gợi ý lời giải:

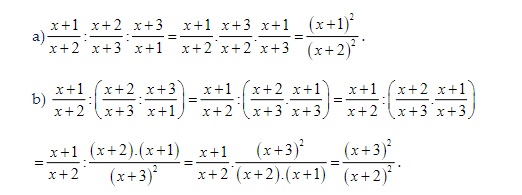
Kết luận

Phép chia phân thức là một khái niệm trọng trong đại số và là một phần quan trọng của chương trình toán lớp 8. Trong bài viết này, thayphu đã cùng các bạn tìm hiểu về phép chia phân thức, cách thực hiện phép chia và đã xem qua một số ví dụ minh họa cũng như các dạng toán khác nhau của nó. Hy vọng rằng các bạn đã có một cái nhìn tổng quan về chủ đề này và có thể áp dụng kiến thức này vào việc giải các bài tập và áp dụng chúng vào các dạng toán nâng cao hơn nữa nhé.