Công thức phân tích đơn thức thành nhân tử và cách nhận biết

Phân tích đơn thức thành nhân tử là quá trình chia một đơn thức thành tích của các đơn thức nhỏ hơn.Định nghĩa , ví dụ minh hoạ

Phân tích đơn thức thành nhân tử là một quá trình quan trọng trong toán học giúp chúng ta hiểu rõ hơn về cấu trúc và phân tích của biểu thức đa thức. Đơn thức là một khái niệm cơ bản trong đại số đa thức và biểu thị một biểu thức toán học chỉ chứa một biến và các hệ số nhân với biến đó.

Trong bài viết này chúng ta sẽ cùng thayphu tìm hiểu những kiến thức cơ bản và các phương pháp quan trọng của việc phân tích thành nhân tử đơn thức.

Định nghĩa về phân tích đơn thức thành nhân tử

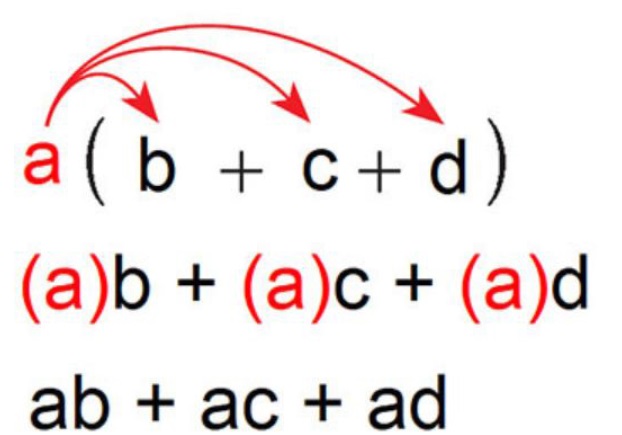
Định nghĩa về phân tích đơn thức thành nhân tử

Đơn thức là một biểu thức toán học chỉ chứa một biến và các hệ số nhân biến đó. Phân tích một đơn thức thành nhân giúp chúng ta chia một biểu thức đa thức phức tạp thành các thành phần nhỏ hơn, giúp chúng ta hiểu rõ hơn về cấu trúc của biểu thức và thực hiện các phép tính đa thức dễ dàng hơn.

Những quy tắc khi phân tích đơn thức thành nhân tử

Khi phân tích các đơn thức, có một số quy tắc cơ bản chúng ta có thể áp dụng.

Sau đây là một số quy tắc chung để phân tích thành nhân tử đơn thức:

Quy tắc rút gọn

Kiểm tra xem đơn thức có thể rút gọn được hay không bằng cách chia tất cả các hệ số và biến chung. Ví dụ: đơn thức 6x^2y^3 có thể được rút gọn thành 2xy^3.

Quy tắc tách biến

Kiểm tra xem biến có thể được tách khỏi đơn thức hay không. Ví dụ, đơn thức 3xy có thể được chia thành xy.

Quy tắc phân tích với công thức khai triển

Sử dụng công thức khai triển làm công thức nhân đa thức (ví dụ: Công thức nhân đa thức Newton).

Quy tắc nhân đa thức

Áp dụng quy tắc nhân đa thức để nhân các đơn thức với nhau.Ví dụ: (2x)(3xy) = 6x^2y.

Quy tắc nhân tử chung

Nếu trong các đơn thức có một đơn thức chung thì ta có thể nhân thừa số chung và giữ nguyên số mũ của biến chung. Ví dụ: (2x)(3x^2) = 6x^3.

Công thức phân tích đơn thức thành nhân tử

Công thức phân tích nhân tử hai bình phương: (a^2 - b^2) = (a + b)(a - b).

Các công thức giai thừa khác nhau: (a - b)(c - d) = ac - ad - bc + bd.

Công thức hệ số hiệu bậc hai: (a^2 – b^2)(c – d) = (a + b)(a – b)(c – d).

Cách phân tích một đơn thức thành nhân tử

Để phân tích một đơn thức, bạn cần tìm các ước chung của các thành phần của đơn thức đó. Dưới đây là cách phân tích một đơn thức:

Kiểm tra xem đơn thức có khả năng rút gọn hay không

Đôi khi một đơn thức có thể được rút gọn về dạng tổng quát hơn. Ví dụ: đơn thức x^2 + 2x + 1 có thể được đơn giản hóa thành (x + 1)^2. 2.

Tìm ước chung

Xác định ước chung của các thành phần của đơn thức. Điều này bao gồm việc tìm kiếm các thừa số chung trong các hệ số và số mũ của các biến. Ví dụ, chúng ta có thể đơn giản hóa đơn thức 3x^2 + 6x thành 3x(x + 2), trong đó 3x là ước chung.

Rút gọn đơn thức

Rút gọn đơn thức về dạng giai thừa theo các nhân tử chung tìm được. Ví dụ: đơn thức x^2 + 4x + 4 có thể được đơn giản hóa thành (x + 2)(x + 2) hoặc (x + 2)^2.

Cách nhận biết một số để phân tích thành nhân tử

Để xác định một số có thể phân tích thành nhân tử, bạn có thể sử dụng các phương pháp sau:

Phân tích thừa số nguyên tố

Một số nguyên dương n có thể được phân tích thành thừa số nếu n không phải là số nguyên tố. Để phân tích thành thừa số nguyên tố, hãy đảm bảo rằng n có thể chia cho các số nguyên dương nhỏ hơn n mà không có số dư. Nếu bạn tìm thấy một số nguyên dương khác 1, khác với n và chia hết cho n thì n có thể được phân tích thành thừa số.

Kiểm tra mẫu số

Một số có thể được phân tích thành nhân tử nếu nó là phân số tối giản và tử số và mẫu số không có ước chung. Bạn hãy cố gắng chuyển phân số về dạng phân tích nhân tử bằng cách phân tích cả tử số và mẫu số.

Sử dụng phân tích đa thức

Nếu số được biểu thị dưới dạng đa thức, bạn có thể sử dụng phương pháp phân tích đa thức để xác định xem nó có thể được phân tích thành nhân tử hay không. Điều này bao gồm việc sử dụng các phương trình và phương pháp đa thức như phân tích nghiệm, sử dụng định lý phân tích nhân tử hoặc áp dụng các công thức như công thức phân tích nhân tử của Viète.

Sử dụng công thức và quy tắc phân tích

Một số có thể được phân tích thành nhân tử bằng các công thức và quy tắc phân tích như công thức Newton, quy tắc phân tích nhân tử cho đa thức bậc hai và bậc ba hoặc các quy tắc phân tích đặc biệt như trích thể tích hoặc khai triển nhị thức.

Một số dạng toán về phân tích một đơn thức thành nhân tử

Dưới đây là một số dạng toán liên quan đến phân tích nhân tử của một đơn thức:

Phân tích thành nhân tử của một đơn thức bình phương

Một đơn thức bình phương có dạng ax^2 + bx + c, trong đó a, b và c là các hệ số thực và a về cơ bản là khác biệt. Bạn có thể sử dụng công thức phân tích nhân tử của Viète hoặc quy tắc phân tích nhân tử đa thức bậc hai để phân tích đơn thức này. Ví dụ: x^2 + 5x + 6 = (x + 2)(x + 3).

Phân tích đơn thức bậc ba

Đơn thức bậc ba có dạng ax^3 + bx^2 + cx + d, trong đó a, b, c và d là các hệ số thực và a khác 0. Bạn có thể sử dụng công thức nhân tử Viète hoặc công thức quy tắc bậc ba của nhân tử đa thức để phân tích đơn thức này. Ví dụ: x^3 - 8 = (x - 2)(x^2 + 2x + 4).

Phân tích đơn thức đa biến

Đơn thức nhiều biến là đơn thức có nhiều hơn một biến.Phân tích đơn thức thành nhân tử thường được thực hiện thông qua việc áp dụng các phương pháp phân tích đa thức, chẳng hạn như sử dụng phương trình đa thức và công thức phân tích đa thức. Ví dụ: x^2y + xy^2 - x^2 - y^2 = (x - y)(xy - x - y).

Phân tích một đơn thức có thừa số chung

Nếu một đơn thức có các biến có chung một thừa số thì có thể phân tích thành nhân tử bằng cách tách các thừa số chung của đơn thức đó. Ví dụ: 3x^2 + 6x = 3x(x + 2).

Phân tích đơn thức bằng công thức

Đôi khi một đơn thức có thể được phân tích thành nhân tử bằng các công thức như công thức Newton hoặc khai triển nhị thức. Ví dụ: x^3 - 1 = (x - 1)(x^2 + x + 1).

Một số lưu ý khi phân tích một đơn thức thành nhân tử

Khi phân tích một đơn thức thành nhân tử, dưới đây là một số lưu ý quan trọng:

• Kiểm tra tính rút gọn: Trước khi phân tích đơn thức thành nhân tử, hãy kiểm tra xem đơn thức đã được rút gọn hoàn toàn hay chưa. Nếu đơn thức có thể được rút gọn về dạng đơn giản hơn thì hãy làm như vậy trước khi phân tích nhân tử.
• Tìm thừa số chung: Xác định các thừa số chung của đơn thức cần phân tích thành nhân tử.Điều này bao gồm việc tìm kiếm các thừa số chung trong các hệ số và số mũ của các biến. Bằng cách tìm các thừa số chung, bạn có thể phân tích thành thừa số đơn thức dễ dàng hơn.
• Sử dụng phương trình đa thức: Trong một số trường hợp, việc sử dụng phương trình đa thức có thể hữu ích trong việc xác định thừa số đơn thức. Bằng cách giải phương trình đa thức tương ứng, bạn có thể xác định giá trị của các biến có đơn thức bằng 0, từ đó tìm ra các thừa số.

Bài tập áp dụng

Bài tập 1:Phân tích đơn thức x^4 + 6x^2 + 9 thành nhân tử.

Đáp án:

x^4 + 6x^2 + 9 = (x^2 + 3)^2

Bài tập 2:Phân tích đơn thức 4x^3 - 8x^2 + 4x thành nhân tử.

Đáp án:

4x^3 - 8x^2 + 4x = 4x(x - 1)^2

Bài tập 3:Phân tích đơn thức 2x^5 - 32x^3 + 16x thành nhân tử.

Đáp án:

2x^5 - 32x^3 + 16x = 2x(x - 2)(x + 2)(x^2 + 4)

Bài tập 4:Phân tích đơn thức x^6 - 64 thành nhân tử.

Đáp án:

x^6 - 64 = (x^2 - 2x + 4)(x^4 + 2x^3 + 4x^2 + 8x + 16)

Bài tập 5:Phân tích đơn thức 3x^4 - 12x^3 + 12x^2 - 4x thành nhân tử.

Đáp án:

3x^4 - 12x^3 + 12x^2 - 4x = 3x(x - 1)^3

Bài tập 6:Phân tích đơn thức x^5 - 25x thành nhân tử.

Đáp án:

x^5 - 25x = x(x - 5)(x + 5)(x^2 + 5)

Bài tập 7:Phân tích đơn thức 4x^4 - 16x^2 + 16 thành nhân tử.

Đáp án:

4x^4 - 16x^2 + 16 = 4(x^2 - 2)^2

Bài tập 8:Phân tích đơn thức x^7 - 64x^3 + 64 thành nhân tử.

Đáp án:

x^7 - 64x^3 + 64 = (x - 2)(x + 2)(x^2 + 4)(x^4 + 2x^3 + 4x^2 + 8x + 16)

Kết luận

Hy vọng những bài tập về phân tích đơn thức thành nhân tử đã giúp bạn ôn tập và nắm vững phương pháp này. Phân tích đơn thức thành nhân tử là một kỹ năng quan trọng trong đại số và đóng vai trò quan trọng trong việc giải các bài toán đa thức phức tạp.