Lũy thừa với số mũ tự nhiên được hiểu như thế nào?

Lũy thừa với số mũ tự nhiên là một khái niệm cơ bản đóng vai trò quan trọng trong nhiều lĩnh vực khác nhau.Định nghĩa, tính chất, bài tập áp dụng.

Trong toán học,lũy thừa với số mũ tự nhiên là một khái niệm quan trọng và phổ biến được áp dụng trong nhiều lĩnh vực, từ đại số, hình học cho đến khoa học máy tính. Hiểu và biểu diễn các phép tính phức tạp khi sử dụng lũy thừa mũ mang lại sự tiện lợi và hiệu quả cao.

Trong bài viết này của thayphu sẽ khám phá sâu hơn về lũy thừa, từ các khái niệm cơ bản đến ứng dụng thực tế. Chúng ta sẽ tìm hiểu các quy tắc và tính chất quan trọng của lũy thừa với số mũ tự nhiên , cùng với ví dụ và bài toán thú vị để nắm vững khái niệm này.

Định nghĩa về lũy thừa với số mũ tự nhiên trong toán học

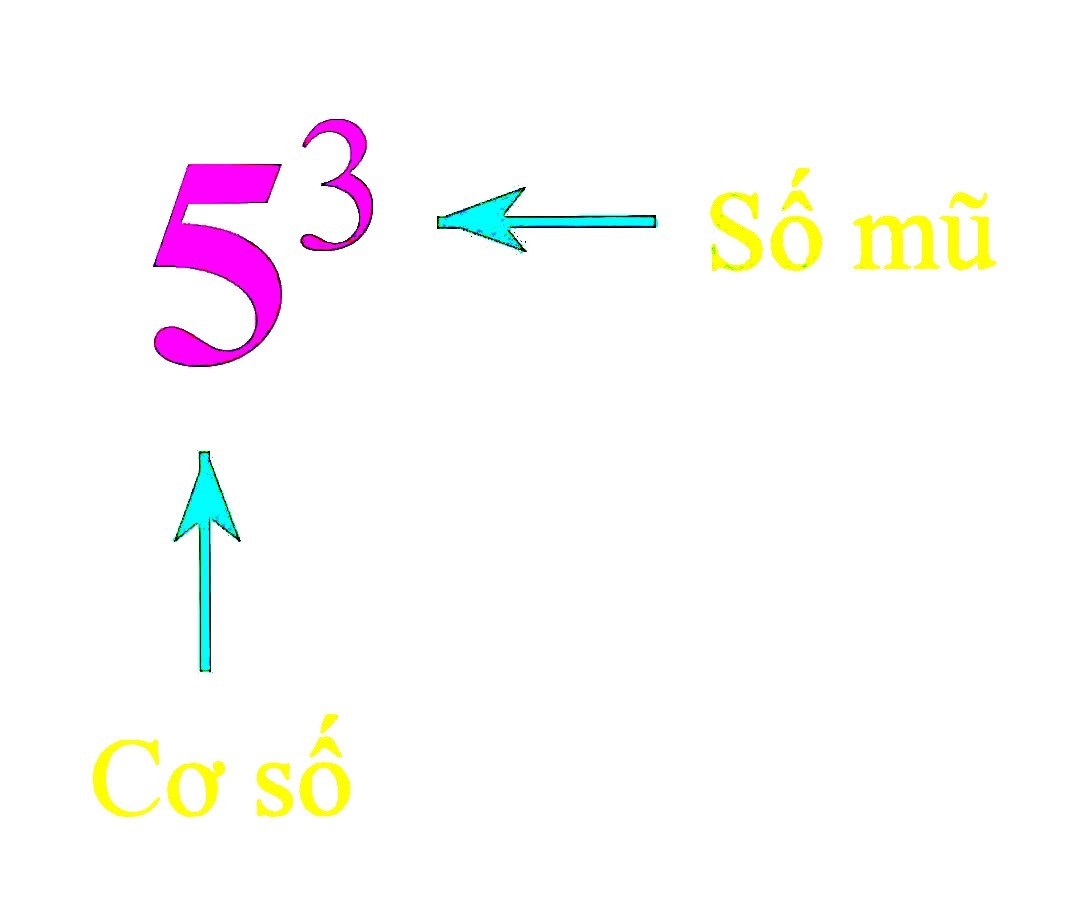
Định nghĩa về lũy thừa với số mũ tự nhiên trong toán học

Lũy thừa với số mũ tự nhiên là một phép tính toán học trong đó một số được nhân với chính nó nhiều lần dựa trên số mũ là số nguyên dương.

Đây là một khái niệm cơ bản và quan trọng trong đại số và toán học đại cương.

Để biểu diễn lũy thừa bằng số mũ tự nhiên,ta dùng ký hiệu a^n, trong đó a là cơ số và n là số mũ.

Nếu nhân a với chính nó n lần thì kết quả gọi là lũy thừa của a với số mũ n.

Công thức lũy thừa với số mũ tự nhiên được xác định như sau: a^n = a × a × a × ... × a (nhân n lần)

Ở đây a được nhân với chính nó n lần. Ví dụ: 2^3 = 2 × 2 × 2 = 8, 3^4 = 3 × 3 × 3 × 3 = 81.

Tính chất của lũy thừa với số mũ tự nhiên

Các lũy thừa với số mũ tự nhiên có nhiều tính chất quan trọng và hữu ích trong toán học. Dưới đây là một số tính chất chính của lũy thừa với số mũ tự nhiên:

• Quy tắc nhân: Khi nhân hai lũy thừa cùng cơ số, a^m × a^n = a^(m + n). Điều này có nghĩa là khi nhân hai lũy thừa cùng cơ số, chúng ta có thể cộng các số mũ.
• Ví dụ: 2^3 × 2^4 = 2^(3 + 4) = 2^7 = 128.
• Quy tắc chia : Khi chia hai lũy thừa cùng cơ số, a^m/a^n = a^(m - n). Điều này có nghĩa là khi chia hai lũy thừa có cùng cơ số, chúng ta có thể trừ số mũ của chúng.
• Ví dụ: 5^6 / 5^2 = 5^(6 - 2) = 5^4 = 625
• Quy tắc lũy thừa: Nếu có một lũy thừa mà số mũ của nó là một lũy thừa khác thì (a^m)^n = a^(m × n). Điều này có nghĩa là bằng cách nâng lũy ​​thừa lên lũy thừa, chúng ta có thể nhân số mũ của nó.Ví dụ: (3^2)^3 = 3^(2 × 3) = 3^6 = 729.
• Quy tắc lũy thừa 1: Mọi số lũy thừa 1 đều bằng chính nó, a ^1 = a.Ví dụ: 4^1 = 4. 5. Quy tắc lũy thừa 0: Khi một số cơ sở khác 0 được nâng lên số mũ bằng 0, ta có a^0 = 1.

Tuy nhiên, không có quy tắc nào rõ ràng áp dụng cho 0 ^0 và giá trị này thường được coi là không xác định.

• Ví dụ: 2^0 = 1. Các thuộc tính trên chỉ là một vài ví dụ phổ biến. Các lũy thừa và số mũ tự nhiên còn có nhiều tính chất khác, có thể kết hợp và áp dụng để giải các bài toán phức tạp trong toán học và các lĩnh vực liên quan.

Các thứ tự ưu tiên được thực hiện trong phép toán lũy thừa với số mũ tự nhiên

Trong toán học, có một số quy tắc liên quan đến thứ tự ưu tiên khi thực hiện các phép toán. Thứ tự ưu tiên giúp xác định thứ tự thực hiện các phép toán trước để đảm bảo tính chính xác của kết quả. Đây là các quy tắc ưu tiên thông thường:

• Dấu ngoặc: Các thao tác trong ngoặc được thực hiện trước. Nếu có nhiều cặp dấu ngoặc thì đếm từ trong ra ngoài.
• Số mũ và căn bậc hai: Các phép tính số mũ và căn bậc hai được thực hiện sau dấu ngoặc đơn. Chúng được tính từ trái sang phải. Ví dụ: 2^3^2 được tính là 2^(3^2), không phải (2^3)^2.
• Phép nhân và chia: Phép nhân và chia được thực hiện bằng cách sử dụng lũy ​​thừa và căn bậc hai. Chúng cũng được tính từ trái sang phải. Ví dụ: 4 ` 2 × 3 được tính là (4 ` 2) × 3 chứ không phải 4 ` (2 × 3).
• Phép cộng và phép trừ: Phép cộng và phép trừ là các phép toán được thực hiện cuối cùng.Chúng cũng được tính từ trái sang phải. Ví dụ: 5 + 3 - 2 được tính là (5 + 3) - 2 chứ không phải 5 + (3 - 2).

Một số dạng bài toán về lũy thừa với số mũ tự nhiên

Một số dạng bài toán về lũy thừa với số mũ tự nhiên

Dưới đây là một số bài toán thường gặp liên quan đến lũy thừa với số mũ tự nhiên:

• Tính giá trị lũy thừa: Bài này yêu cầu tính giá trị của lũy thừa với số mũ tự nhiên cho trước. Ví dụ: tính giá trị của 2^5, 3^4 hoặc 10^3.
• Quy tắc nhân chia: Áp dụng quy tắc nhân chia để đơn giản hóa các biểu thức chứa lũy thừa.Ví dụ: rút gọn biểu thức 2^3 × 2^2 thành dạng đơn giản hơn.
• Lũy thừa của lũy thừa: Bài toán tính giá trị của một lũy thừa có số mũ là lũy thừa khác. Ví dụ: tính giá trị của (2^3)^2 hoặc (3^2)^4.
• Số thừa số của một lũy thừa: Bài toán là tìm số thừa số của một lũy thừa. Ví dụ: tìm ước số của 2^4 hoặc 5^3.
• Chứng minh tính chất lũy thừa: Cần chứng minh tính chất hoặc quy luật liên quan đến lũy thừa. Ví dụ: Nêu quy tắc nhân lũy thừa.
• Định thức số mũ: Yêu cầu xác định chữ số cuối cùng của lũy thừa lớn. Ví dụ: tìm chữ số cuối cùng của 2^1000.
• Số mũ đặc biệt: Nhắc bạn tìm giá trị lũy thừa với số mũ đặc biệt, ví dụ: Ví dụ: lũy thừa bằng 0, lũy thừa bằng 1 hoặc lũy thừa bằng số chẵn.Ví dụ: tính giá trị của 2^0, 3^1, 4^2.

Bài tập áp dụng

• Bài tập 1:

Tính giá trị của 2^4.

Đáp án: 2^4 = 2 × 2 × 2 × 2 = 16.

• Bài tập 2:

Rút gọn biểu thức 5^3 × 5^2.

Đáp án: 5^3 × 5^2 = 5^(3 + 2) = 5^5.

• Bài tập 3:

Tính giá trị của (3^2)^3.

Đáp án: (3^2)^3 = 3^(2 × 3) = 3^6.

• Bài tập 4:

Tính số ước của 2^4.

Đáp án: Số ước của 2^4 là 5 (1, 2, 4, 8 và 16).

• Bài tập 5:

Chứng minh rằng (a^m)^n = a^(m × n) với a, m, n là số nguyên dương.

Đáp án: Ta có (a^m)^n = a^(m × n) với a, m, n là số nguyên dương.

• Bài tập 6:

Tìm chữ số cuối cùng của 3^100.

Đáp án: Chữ số cuối cùng của 3^100 là 1.

• Bài tập 7:

Tính giá trị của 2^0.

Đáp án: 2^0 = 1.

• Bài tập 8:

Tìm số ước của 7^4.

Đáp án: Số ước của 7^4 là 5 (1, 7, 49, 2401 và 16807).

• Bài tập 9:

Tính giá trị của 4^0 × 4^3.

Đáp án: 4^0 × 4^3 = 4^(0 + 3) = 4^3.

• Bài tập 10:

Tính giá trị của (5^2)^4 - (5^4)^2.

Đáp án: (5^2)^4 - (5^4)^2 = 5^(2 × 4) - 5^(4 × 2) = 5^8 - 5^8 = 0.

Trên đây là những thông tin mà về lũy thừa với số mũ tự nhiên. Chúng ta đã tìm hiểu về các quy tắc và tính chất quan trọng của lũy thừa, từ việc tính giá trị đơn giản đến rút gọn biểu thức phức tạp hơn.