Hình thang cân: tính chất, cách nhận biết và công thức tính

Hình thang cân là gì? Nó là một hình học hai chiều được tạo từ bốn cạnh khác nhau, xem cách tính diện tích và chu vi hình thang cân tại đây.

Hình thang cân, một thuật ngữ nổi tiếng trong hình học, là một hình hình học đặc biệt có những đặc tính vượt trội và hứa hẹn nhiều ứng dụng thú vị. Trong bài viết này hãy cùng thayphu khám phá hình thang cân là gì? một dạng hình học thú vị!

Định nghĩa và đặc điểm hình thang cân đặc biệt

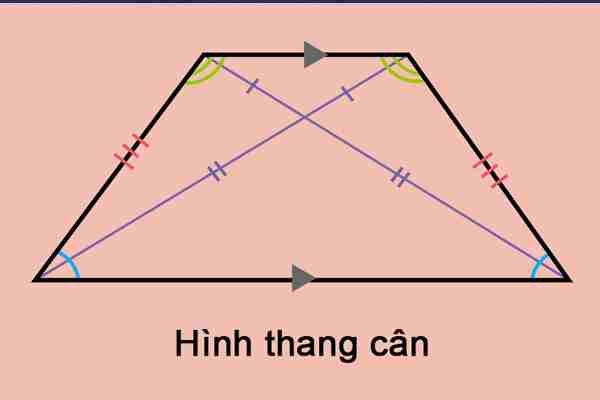
Định nghĩa và đặc điểm của một hình thang cân đặc biệt

Hình thang cân là một hình hình học hai chiều bao gồm bốn cạnh, hai cạnh đối diện song song và có chiều dài bằng nhau.

Ngoài ra, hai cạnh còn lại cũng có thể có độ dài khác nhau. Hình thang cân có hai cặp góc đối xứng nhau, tức là hai góc giữa hai cạnh song song có giá trị bằng nhau. Các góc khác của hình thang cân không nhất thiết phải có cùng giá trị.

Đặc điểm nổi bật của hình thang cân là có một trục đối xứng thẳng đứng đi qua trung điểm của hai cạnh đáy gọi là trục đối xứng chính.Điều này có nghĩa là hình thang cân chia thành hai phần đối xứng khi bạn vẽ một đường thẳng qua trục đối xứng chính.

Tính chất đặc trưng hình thang cân đặc biệt

Hình thang cân có một số tính chất đáng chú ý:

• Hai cạnh đáy song song và bằng nhau: Hình thang cân có hai cạnh đáy song song và dài bằng nhau. Điều này có nghĩa là hai đường thẳng song song chạy qua các điểm góc của hình thang cân có độ dài bằng nhau.
• Các cạnh bằng nhau: Hai cạnh của hình thang cân có độ dài bằng nhau.Điều này tạo ra sự đối xứng và cân bằng giữa các cạnh của hình thang.
• Hai cặp góc đối xứng: Một hình thang cân có hai cặp góc đối xứng nhau, tức là hai góc xen giữa hai cạnh đáy có giá trị bằng nhau.
• Trục đối xứng chính: Hình thang cân có trục đối xứng chính đi qua trung điểm hai cạnh đáy.

Công thức tính chu vi và diện tích hình thang cân

Công thức tính chu vi và diện tích của một hình thang cân như sau:

Chu vi (P):

Chu vi của hình thang cân bằng tổng độ dài của tất cả các cạnh.

P = (đáy nhỏ + đáy lớn + cạnh bên 1 + cạnh bên 2)

Diện tích (S):

Diện tích của hình thang cân có thể được tính bằng công thức:

S = ((đáy nhỏ + đáy lớn) * chiều cao) / 2

Trong đó:

Đáy nhỏ và đáy lớn là độ dài của hai cạnh đáy.

Chiều cao là khoảng cách vuông góc giữa hai cạnh đáy.

Công thức tính diện tích hình thang cân đặc biệt

Để chứng minh công thức tính diện tích hình thang cân, chúng ta có thể sử dụng phương pháp hình học hoặc tích phân.

Trong trường hợp này chúng tôi sử dụng phương pháp hình học.

Giả sử chúng ta có một hình thang cân có đáy nhỏ dài a, đáy lớn dài b và chiều cao h. Để chứng minh công thức diện tích, chúng ta chia hình thang thành hai hình tam giác, tính diện tích mỗi tam giác rồi cộng chúng lại với nhau.

Tam giác 1 có đáy nhỏ a và chiều cao h.Do đó, diện tích tam giác 1 là:

S1 = (1/2) * a * h

Tam giác 2 có đáy b lớn và chiều cao h.

Do đó, diện tích tam giác 2 là: S2 = (1/2) * b * h

Tổng diện tích của hai tam giác này là: S = S1 + S2 = (1/2) * a * h + (1/ 2) * b * h = (1/2) * (a + b) * h

Như vậy ta đã chứng minh được công thức tính diện tích hình thang cân: S = (1/2) * (a + b ) * h

Đây là công thức chính xác cho diện tích hình thang cân.

Dấu hiệu nhận biết đặc điểm của một hình thang cân trong toán học

Để nhận biết hình thang là hình thang cân, ta có thể dựa vào các dấu hiệu sau:

• Hai cạnh đáy song song và bằng nhau: Một hình thang cân có hai cạnh đáy song song và dài bằng nhau. Nếu các cạnh đáy của hình thang có độ dài khác nhau hoặc không song song thì đó không phải là hình thang cân.
• Tính đối xứng và cân bằng: Một hình thang cân có hai cặp góc đối xứng nhau, nghĩa là hai góc giữa hai cạnh song song của đáy có giá trị bằng nhau.Điều này tạo ra sự cân bằng và đối xứng trong hình thang. Nếu các góc giữa các cạnh của đáy không bằng nhau thì hình thang đó không phải là hình thang cân.
• Trục đối xứng chính: Hình thang cân có trục đối xứng chính đi qua trung điểm hai cạnh đáy. Tức là, nếu vẽ một đường thẳng qua trục đối xứng chính thì hình thang sẽ được chia thành hai phần đối xứng.Nếu không có trục đối xứng chính hoặc hình thang không chia thành hai phần đối xứng thì đó không phải là hình thang cân.

Các phương pháp giải bài toán liên quan đến hình thang cân

Có một số phương pháp để giải các bài toán hình thang cân.

Dưới đây là một số phương pháp phổ biến:

Sử dụng công thức tính diện tích và chu vi

Đối với bài toán hình thang cân, bạn có thể sử dụng công thức tính diện tích và chu vi để giải. Để áp dụng công thức tương ứng, bạn cần biết độ dài các cạnh, đỉnh hoặc chiều cao của hình thang.

Sử dụng tính đối xứng

Hình thang cân là gì? có tính chất đối xứng nên có thể vận dụng tính chất này để giải các bài toán. Đôi khi việc tìm một cạnh, đỉnh hoặc góc đối xứng có thể giúp xác định giá trị cần tìm.

Sử dụng Định lý Pythagore

Nếu bạn có thông tin về các cạnh và các góc của một hình thang cân, bạn có thể áp dụng Định lý Pythagore để tính các giá trị cần tìm. Định lý Pythagore xác định mối quan hệ giữa các cạnh thẳng đứng của một tam giác.

Sử dụng tính đối xứng và tương đương

Đôi khi có thể sử dụng tính đối xứng và tương đương để giải bài toán hình thang cân. Bằng cách thay đổi vị trí của các cạnh, đỉnh hoặc góc, bạn có thể tạo ra các hình thang tương đương dễ tính toán hơn.

Sử dụng hình học không gian

Trong một số trường hợp, bài toán hình thang cân có thể được giải bằng hình học không gian, ví dụ bằng cách sử dụng vectơ hoặc tọa độ trong không gian ba chiều. Với mỗi bài toán cụ thể, phương pháp giải có thể khác nhau tùy theo thông tin cụ thể và yêu cầu của bài toán.

Bài tập áp dụng

Bài tập 1:

Cho một hình thang cân với đáy nhỏ độ dài 6 cm, đáy lớn độ dài 10 cm và chiều cao 8 cm. Tính chu vi và diện tích của hình thang.

Đáp án:

Chu vi: P = 6 + 10 + 8 + 8 = 32 cm

Diện tích: S = ((6 + 10) * 8) / 2 = 64 cm²

Bài tập 2:

Hình thang ABCD có đáy nhỏ AB độ dài 12 cm, đáy lớn CD độ dài 20 cm và chiều cao 10 cm. Tìm độ dài cạnh bên của hình thang.

Đáp án:

Đáy nhỏ AB = 12 cm

Đáy lớn CD = 20 cm

Chiều cao h = 10 cm

Vì hình thang cân, ta có cạnh bên BC = cạnh bên AD.

Bằng định lý Pythagoras, ta có:

BC² = CD² - BD² = 20² - 12² = 400 - 144 = 256

BC = √256 = 16 cm

Vậy cạnh bên của hình thang là 16 cm.

Bài tập 3:

Hình thang PQRS có đáy nhỏ PQ và đáy lớn SR. Đường chéo AC của hình thang cắt đường chéo BD tại điểm O. Biết AC = 12cm, BD = 16cm và AO = 6cm. Tìm độ dài BO.

Đáp án:

Vì hình thang cân, ta có AO = OC và BO = OD.

Áp dụng định lý Pythagore trong tam giác ABO:

AB² = AO² + BO² = 6² + BO²

AB = √(36 + BO²)

Áp dụng định lý Pythagore trong tam giác BCD:

BC² = BD² - CD² = 16² - 12² = 256 - 144 = 112

BC = √112 = 4√7

Vì BC = AB + AC, ta có:

4√7 = √(36 + BO²) + 12

4√7 - 12 = √(36 + BO²)

(4√7 - 12)² = 36 + BO²

112 - 96√7 + 144 = 36 + BO²

BO² = 112 - 96√7 + 144 - 36

BO² = 220 - 96√7

BO ≈ 5.78 cm

Vậy độ dài BO là khoảng 5.78 cm.

Bài tập 4:

Trong hình thang ABCD, đường chéo AC cắt đường chéo BD tại điểm O. Biết AC = 15cm, BD = 20cm và BO = 9cm. Tính độ dài cạnh bên của hình thang.

Đáp án:

Vì hình thang cân, ta có AO = OC và BO = OD.

Áp dụng định lý Pythagore trong tam giác ABO:

AB² = AO² + BO² = 9² + AB²

AB = √(81 + AB²)

Áp dụng định lý Pythagore trong tam giác BCD:

BC² = BD² - CD² = 20² - 15² = 400 - 225 = 175

BC = √175 = √(25 * 7) = 5√7 cm

Vì BC = AB + AC, ta có:

5√7 = √(81 + AB²) + 15

5√7 - 15 = √(81 + AB²)

(5√7 - 15)² = 81 + AB²

175 - 150√7 + 225 = 81 + AB²

AB² = 175 - 150√7 + 225 -64

AB² = 400 - 150√7

AB ≈ 7.74 cm

Vậy độ dài cạnh bên của hình thang là khoảng 7.74 cm.

Bài tập 5:

Hình thang ABCD có đáy nhỏ AB, đáy lớn CD và cạnh bên BC. Biết AB = 10cm, CD = 16cm và BC = 12cm. Tính diện tích của hình thang.

Đáp án:

Vì hình thang cân, ta có cạnh bên BC = cạnh bên AD.

Diện tích hình thang là tổng diện tích hai tam giác ABP và CDP, trong đó P là trung điểm của AD.

Diện tích tam giác ABP:

S₁ = (1/2) * AB * h₁ = (1/2) * 10 * (BC / 2) = 25 cm²

Diện tích tam giác CDP:

S₂ = (1/2) * CD * h₂ = (1/2) * 16 * (BC / 2) = 48 cm²

Diện tích của hình thang:

S = S₁ + S₂ = 25 + 48 = 73 cm²

Vậy diện tích của hình thang là 73 cm².

Bài tập 6:

Cho hình thang ABCD với đáy nhỏ AB và đáy lớn CD. Biết rằng AB = 12 cm, CD = 20 cm, và chiều cao h = 8 cm. Tính chu vi của hình thang.

Đáp án:

Vì hình thang cân, ta có cạnh bên BC = cạnh bên AD.

Chu vi của hình thang là tổng độ dài các cạnh.

Chu vi = AB + BC + CD + AD

Chu vi = 12 + BC + 20 + BC

Chu vi = 32 + 2BC

Để tính chu vi, cần tìm giá trị của BC.

Áp dụng định lý Pythagore trong tam giác BCD:

BC² = CD² - BD² = 20² - h² = 400 - 64 = 336

BC = √336 = 4√21 cm

Chu vi = 32 + 2(4√21) = 32 + 8√21 ≈ 57.05 cm

Vậy chu vi của hình thang là khoảng 57.05 cm.

Bài tập 7:

Hình thang ABCD có đáy nhỏ AB và đáy lớn CD. Biết rằng AB = 18cm, CD = 30cm, và chu vi của hình thang là 76cm. Tính chiều cao của hình thang.

Đáp án:

Vì hình thang cân, ta có cạnh bên BC = cạnh bên AD.

Chu vi của hình thang là tổng độ dài các cạnh.

Chu vi = AB + BC + CD + AD

76 = 18 + BC + 30 + BC

76 = 48 + 2BC

2BC = 76 - 48 = 28

BC = 28 / 2 = 14 cm

Vì BC = AD, ta có chiều cao h bằng độ dài BC.

Vậy chiều cao của hình thang là 14 cm.

Kết luận

Trong bài viết trên, chúng ta đã khám phá và giải quyết một số bài tập tự luận liên quan đến hình thang cân là gì? Chúng ta đã tìm ra các giá trị của chu vi, diện tích, độ dài cạnh bên và chiều cao của hình thang dựa trên các thông số như đáy nhỏ, đáy lớn và cạnh bên. Bằng cách áp dụng các công thức và định lý hợp lý, chúng ta đã giải quyết những bài toán phức tạp và tìm ra các giá trị cần thiết.