Hai tam giác đồng dạng, phương pháp tính và bài tập

Làm thế nào để chứng minh hai tam giác đồng dạng với nhau? Khái niệm, tính chất và phương pháp chứng minh hai tam giác đồng dạng cùng các dạng toán thường gặp.

Tam giác đồng dạng là một khái niệm thú vị và quan trọng trong hình học, được áp dụng trong nhiều lĩnh vực khác nhau. Trong chương trình toán ở cấp trung học cơ sở thì đây là khái niệm khá trọng tâm và hay xuất hiện trong các đề thi. Trên cơ sở của sự tương đồng hình học, hai tam giác đồng dạng có thể có các góc tương đồng và tỷ lệ giữa các cạnh tương ứng bằng nhau.

Trong bài viết này, hãy cùng thayphu tìm hiểu về định nghĩa và tính chất của hai tam giác đồng dạng, phương pháp chứng minh, cũng như các dạng bài tập vận dụng nhé.

Lý thuyết hai tam giác đồng dạng

Khái niệm

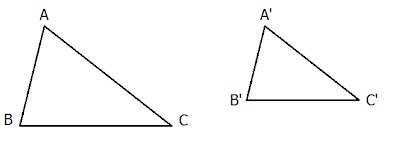
Hai tam giác được coi là đồng dạng nếu chúng có các cặp góc tương đồng và tỷ lệ giữa các cạnh tương ứng bằng nhau.

Nói cách khác, hai tam giác sẽ đồng dạng nếu chúng có ba cặp góc bằng nhau từng đôi một và ba cặp cạnh tương ứng tỉ lệ.

Ký hiệu: △ABC ~ △A’B’C’ (đọc là tam giác ABC đồng dạng với tam giác A’B’C’).

Định lí

Nếu một đường thẳng song song với 1 cạnh của tam giác và cắt hai cạnh còn lại thì đường thẳng đó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Ví dụ: Cho △ABC, MN//BC

⇒ △ABC ~ △AMN

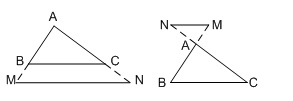
Chú ý:Định lí vẫn đúng khi đường thẳng song song cắt phần kéo dài của hai cạnh tam giác.

Tính chất

Khi tam giác ABC đồng dạng với tam giác A’B’C’ thì ta có các tính chất như sau:

Tính chất tương tự: Hai tam giác đồng dạng có các góc tương đồng. Nghĩa là các góc tương ứng của hai tam giác đồng dạng có giá trị bằng nhau.

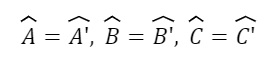
Tính chất tỉ lệ: Trong hai tam giác đồng dạng, tỷ lệ giữa độ dài các cạnh tương ứng là như nhau.

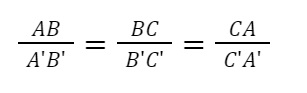
Phương pháp chứng minh các trường hợp tam giác đồng dạng

Trường hợp: Cạnh - Cạnh - Cạnh

Hai tam giác có ba cặp cạnh tỉ lệ với nhau thì được gọi là hai tam giác đồng dạng.

Để chứng minh được trường hợp này, nếu ta chứng minh được:

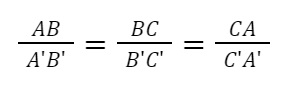
→ chúng ta có thể kết luận 2 tam giác đồng dạng.

Ví dụ: Tam giác ABC và tam giác DEF có kích thước các cạnh như hình minh họa ở dưới. Hãy chứng minh rằng: △ABC ∽ △DEF.

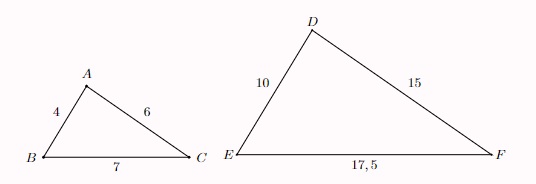
Xét △ABC và △DEF, ta có:

AB/DE = BC/EF = CA/DF

⇔ 4/10 = 7/17,5 = 6/15 = 0,4

⇒ △ABC ∽ △DEF (c.c.c)

Trường hợp: Cạnh - góc - cạnh

Hai tam giác có hai cặp cạnh tỉ lệ với nhau và cặp góc xen giữa chúng bằng nhau thì được gọi là hai tam giác đồng dạng.

Để chứng minh được trường hợp này, nếu ta chứng minh được:

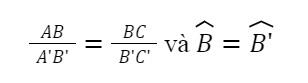
→ chúng ta có thể kết luận 2 tam giác đồng dạng.

Ví dụ: Ta có hai tam giác ADE và ACF có các kích thước như hình minh họa ở dưới. Hãy chứng minh rằng: △ADE ∽ △ACF.

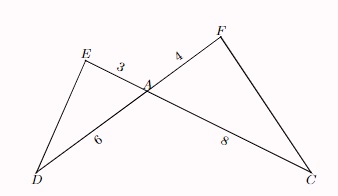
Xét △ADE và △ACF, ta có:

∠EAD = ∠FAC (đối nhau)

AE/AF =AD/AC ⇔ ¾ = 6/8 = 0,75

⇒ △ADE ∽ △ACF (c.g.c)

Trường hợp: Góc - góc

Hai tam giác có hai cặp góc tương ứng bằng nhau thì là hai tam giác đồng dạng.

Để chứng minh được trường hợp này, nếu ta chứng minh được:

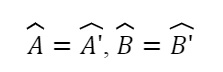
→ chúng ta có thể kết luận 2 tam giác đồng dạng.

Ví dụ: Cho hình minh họa như hình dưới đây, biết AD // BC, BE // DC. Hãy chứng minh rằng: △ADC ∽ △CBE.

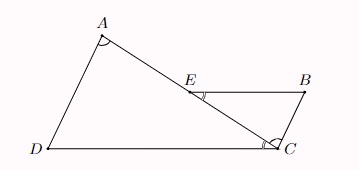
Xét △ADC và △CBE, ta có:

AD // BC ⇔ ∠DAC = ∠BCE (so le trong)

BE // DC ⇔ ∠DCA = ∠BEC (so le trong)

⇒ △ADC ∽ △CBE (g.g)

Các dạng toán thường gặp

Dạng 1: Chứng minh hai tam giác đồng dạng và tính tỉ số đồng dạng của chúng

Phương pháp: Áp dụng định lí và tính chất của hai tam giác đồng dạng để giải dạng toán này.

Ví dụ: Hãy chứng minh hai tam giác sau đây đồng dạng và tính tỉ số đồng dạng của chúng.

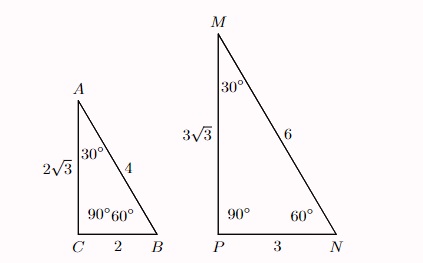
Gợi ý lời giải:

Xét △ABC và △MNP, ta có:

AB/MP = BC/NP = 2√3/3√3 = ⅔

∠ACB = ∠MPN = 90°

⇒ △ABC ∽ △MNP (c.g.c) và tỉ số đồng dạng của hai tam giác là ⅔.

Dạng 2: Dựa vào tam giác đồng dạng để tính góc và độ dài đoạn thẳng

Phương pháp: Áp dụng các tính chất của tam giác đồng dạng, từ đó ta suy ra góc và độ dài đoạn thẳng cần tìm.

Ví dụ: Có △ABC ∽ △A’B’C’ như hình. Hãy tìm x.

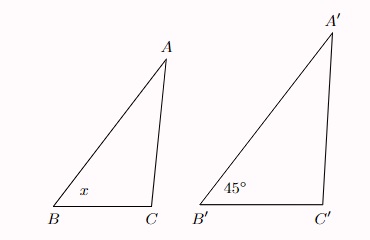
Gợi ý lời giải:

Có △ABC ∽ △A’B’C’.

Dựa vào tính chất của hai tam giác, ta có thể suy ra: ∠ABC = ∠A’B’C.

Mà ∠A’B’C = 45° ⇒ ∠ABC = x = 45°

Vậy x = 45°.

Kết luận

Trong chương trình Toán ở cấp trung học cơ sở, có thể nói khái niệm về hai tam giác đồng dạng là một trong những khái niệm quan trọng trong hình học. Ta cần áp dụng các quy tắc và tính chất của chúng để giải quyết các bài toán liên quan đến tỉ lệ đồng dạng giữa các đường thẳng và độ dài các cạnh. Đây là một dạng toán khá thú vị và xuất hiện rất nhiều trong đề thi cuối kì vì đây là dạng toán trọng tâm. Vì vậy, ta hiểu biết và nắm rõ định nghĩa, các tính chất và phương pháp chứng minh của hai tam giác đồng dạng để dễ dàng giải được các bài toán ở dạng nâng cao hơn.