Cách tính đường trung bình của tam giác và bài tập

Đường trung bình của tam giác là một thuộc tính đặc biệt của tam giác, được tính bằng từ một đỉnh của tam giác đến trung điểm của cạnh đối diện.

Trong hình học, hình tam giác là một khái niệm cơ bản và được nghiên cứu rộng rãi. Một trong những tính chất quan trọng của tam giác là đường trung tuyến, một khái niệm đơn giản nhưng có nhiều ứng dụng thú vị. Trong bài viết này, thayphu xem xét đường trung bình của tam giác,hiểu định nghĩa và tính chất của nó, đồng thời đưa ra một số ví dụ minh họa để minh họa rõ hơn khái niệm này.

Đường trung bình hay được gọi là đường gì?

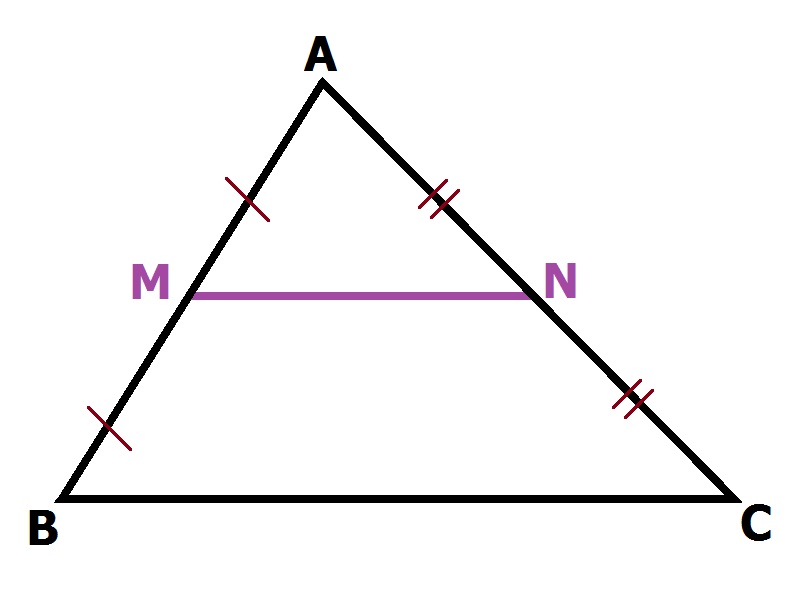
Đường trung bình hay được gọi là đường gì?

Đường trung bình của tam giác hay còn gọi là đường trung tuyến là một khái niệm quan trọng trong hình học tam giác.

Là đường nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Đường trung bình chia cạnh đối diện thành hai đoạn bằng nhau và cắt chúng tại một điểm trên đường trung tâm của tam giác.

Đường trung tuyến thường được biểu thị bằng chữ in hoa, ví dụ: đường trung tuyến AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC. Tương tự như vậy, chúng ta có đường trung tuyến BN nối đỉnh B với điểm giữa N của cạnh AC và đường trung tuyến CP nối đỉnh C với điểm giữa P của cạnh AB.

Phân loại đường trung bình trong các tam giác khác nhau

Trong hình học tam giác, có ba loại đường trung tuyến khác nhau, tùy thuộc vào loại tam giác đang xét:

Đường trung bình trong tam giác đều

Trong tam giác đều, các cạnh và các góc có độ dài và giá trị như nhau. Trong một tam giác đều, các đường trung tuyến trùng với đường cao và các đường phân giác của các góc. Do đó, mỗi đường trung tuyến của tam giác cắt nhau tại một điểm duy nhất, gọi là tâm của tam giác.

Đường trung bình trong tam giác vuông

Trong tam giác vuông, đường trung tuyến là đường nối đỉnh của góc vuông với trung điểm của cạnh đối diện. Tam giác vuông có ba đường trung tuyến từ đỉnh góc vuông A đến trung điểm cạnh BC, từ đỉnh góc vuông B đến trung điểm cạnh AC, từ đỉnh góc vuông C đến trung điểm cạnh AB.

Đường trung bình trong một tam giác tổng quát

Trong một tam giác tổng quát, đường trung tuyến là đường nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Tam giác tổng quát có ba đường trung tuyến khác nhau, từ đỉnh A đến trung điểm M cạnh BC, từ đỉnh B đến trung điểm N của cạnh AC và từ đỉnh C đến trung điểm P của cạnh AB.

Tính chất đường trung bình trong tam giác

Tính chất của các đường trung tuyến trong các tam giác có thể khác nhau tùy thuộc vào loại tam giác được xem xét.

Dưới đây là một số tính chất tiêu biểu của đường trung tuyến trong một số loại tam giác thường gặp:

Tam giác đều

Đường trung tuyến trong tam giác đều là đường cao và các đường phân giác của các góc. Chúng giao nhau tại một điểm duy nhất, là trọng tâm của tam giác đều.

Các đường tâm của một tam giác đều có độ dài bằng nhau và là các đường trung trực của các cạnh.

Tam giác vuông

Trong tam giác vuông, mỗi đường trung tuyến bằng một nửa chiều cao tương ứng.

Hai đường trung tuyến gần cạnh phải nhất của một tam giác vuông có chiều dài bằng nhau và bằng một nửa chiều dài cạnh phải.

Đường trung bình chung có cạnh hình vuông là chiều cao của tam giác và cắt cạnh hình vuông thành hai đoạn theo tỷ lệ 1:2.

Tam giác tù

Trong một tam giác tù, các đường trung tâm không giao nhau tại một điểm. Chúng có một giao điểm chung, gọi là trọng tâm của tam giác. Đường trung tuyến từ một đỉnh đến trung điểm của cạnh đối diện chia cạnh đó thành hai đoạn bằng nhau.

Đường trung bình của tam giác tù không trùng với đường cao hoặc đường phân giác của các góc.

Cách vẽ một đường trung bình trong một tam giác

Để vẽ đường trung tuyến trong một tam giác ta thực hiện như sau:

• Bước 1: Vẽ tam giác ABC.
• Bước 2: Chọn cạnh bất kỳ của tam giác, ví dụ cạnh AB.
• Bước 3: Từ trung điểm cạnh AB gọi là D vẽ đường thẳng đi qua D và song song với cạnh AC. Đây là đường tâm từ đỉnh A.
• Bước 4: Từ trung điểm của cạnh AB và D vẽ đường thẳng đi qua D và song song với cạnh BC.Đây là đường trung bình của đỉnh B.
• Bước 5: Vẽ đường trung tuyến thứ ba bằng cách nối trung điểm hai cạnh còn lại. Nối trung điểm cạnh AC (ký hiệu E) và trung điểm cạnh BC (ký hiệu F) bằng một đường thẳng. Đây là đường trung bình của đỉnh C. Sau khi làm theo các bước trên, bạn sẽ có được đường trung bình của mỗi đỉnh của tam giác.Đường trung tuyến là đường thẳng đi qua đỉnh và trung điểm của cạnh đối diện.

Công thức tính đường trung bình trong một tam giác

Công thức tính đường trung bình trong một tam giác phụ thuộc vào loại tam giác và tâm của nó. Dưới đây là công thức tổng quát tính đường trung tuyến của các loại tam giác:

Đường trung bình trong một tam giác đều

Trong một tam giác đều, các đường trung tuyến trùng với đường cao và các đường phân giác của các góc. Để tính độ dài đường trung tuyến trong một tam giác đều, bạn có thể sử dụng công thức sau:

Trung tuyến = (2/3) * Chiều cao

Trung tuyến trong tam giác vuông

Trong tam giác vuông, đường trung tuyến là đường thẳng nối đỉnh của góc vuông với trung điểm của cạnh đối diện.Độ dài mỗi đường trung tuyến trong một tam giác vuông bằng một nửa độ dài cạnh đối diện.

Chứng minh đường trung bình trong một tam giác

Các tính chất của đường trung tuyến trong một tam giác có thể được chứng minh bằng các định lý và quy tắc hình học. Dưới đây là chứng minh cơ bản về tính chất của các đường trung tuyến trong tam giác:

Giả sử ta có tam giác ABC có đường trung tuyến nối từ đỉnh A đến trung điểm M của cạnh BC.

Bước 1: Chứng minh rằng đường trung tuyến chia cạnh đối diện thành hai đoạn bằng nhau.

Gọi D là trung điểm của cạnh AB. Sau đó, chúng ta có AM là mức trung bình và DM là mức trung bình khác.

Vì D là trung điểm của AB nên AD = DB.

Ta có: AM = AD + DM (theo tính chất của đường trung bình).

Từ AD = DB ta có: AM = DB + DM - Nhưng DB = AD thì ta có AM = AD + DM = DB + DM = BM. - Khi đó đường tâm AM chia cạnh BC thành hai đoạn có độ dài BM và MC bằng nhau.

Bước 2: Chứng minh rằng các đường trung bình cắt nhau tại một điểm.

Giả sử chúng ta có hai đường trung bình động AM và BN trong tam giác ABC.

Ta cần chứng minh AM và BN cắt nhau tại một điểm duy nhất là trọng tâm G của tam giác.

Để chứng minh điều này chúng ta sử dụng định lý trung điểm.

Áp dụng định lý trung điểm ta biết khối tâm G của tam giác là trung điểm của các đoạn AM và BN.

Vì G nằm trong các đường trung bình động AM và BN, AM và BN cắt nhau tại một điểm là trọng tâm G.

Bằng cách thực hiện các bước trên, ta đã chứng minh được tính chất trung tuyến trong một tam giác bao gồm phép chia cạnh đối diện thành hai đoạn bằng nhau cắt nhau tại một điểm (trọng tâm).

Hướng dẫn các em cách chứng minh một đường trung bình trong tam giác

Dưới đây là hướng dẫn cơ bản chứng minh tính chất trung tuyến trong một tam giác:

Giả sử chúng ta cần chứng minh tính chất trung tuyến AM trong tam giác ABC, trong đó M là trung điểm cạnh BC.

• Bước 1: Viết giả thuyết

Viết các giả định về tam giác ABC và đường trung bình động AM. Ví dụ: AB = AC, M là trung điểm của BC.

• Bước 2: Sử dụng các công thức và định lý hình học.

Sử dụng các công thức và định lý hình học để phân tích tam giác và các thành phần của nó. Ví dụ: công thức tính trung điểm, tỷ lệ cắt, định lý trung điểm, định lý cạnh đôi.

• Bước 3: Chứng minh bằng luận điểm.

Đưa ra luận điểm để chứng minh tính chất của đường trung bình AM.

Ví dụ: Ta sẽ chứng minh rằng đường trung bình AM chia cạnh BC thành hai đoạn bằng nhau.

• Bước 4: Sử dụng các bước logic và tính chất hình học. Áp dụng các bước logic và tính chất hình học để chuyển từ giả định, lập luận đến kết luận.
• Bước 5: Viết kết luận

Tóm tắt kết quả chứng minh và viết kết luận đường trung tuyến AM chia cạnh BC thành hai đoạn bằng nhau.

Một số điều cần lưu ý khi chứng minh đường trung bình trong tam giác

Khi chứng minh tính chất đường trung bình của tam giác, các em cần lưu ý một số điều:

Các giả thuyết: Đầu tiên hãy viết ra các giả thuyết về tam giác và đường tâm mà em cần chứng minh. Điều này sẽ giúp bạn xác định thông tin nào cần được sử dụng trong quá trình kiểm tra.

Định nghĩa: Đảm bảo bạn hiểu rõ định nghĩa đường trung tuyến trong một tam giác.Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện.

Công thức và tính chất: Sử dụng các công thức và tính chất hình học liên quan để phân tích tam giác và đường trung tuyến. Ví dụ: công thức tính tâm điểm, tính chất các đoạn thẳng song song, quan hệ giao điểm, định lý tam giác đồng dạng.

Tính tương đương: Thường xuyên sử dụng các quy tắc và định lý về tính tương đương của đường thẳng và đoạn thẳng. Ví dụ: sự tương đương của đường trung tuyến và chiều cao, đường phân giác của góc hoặc sự tương đương của đoạn thẳng sử dụng định lý trung điểm.

Các bước logic: Sử dụng các bước logic và các quy tắc chứng minh hình học một cách chặt chẽ và logic. Đưa ra các giả định và thông tin đã biết để cung cấp các bước kiểm tra hợp lý và nhất quán. Vẽ: Vẽ hình minh họa sẽ giúp bạn hình dung và giải thích các bước làm bài dễ dàng hơn.

Kết luận: Cuối cùng viết kết luận dựa trên quá trình kiểm tra.Kết luận phải rõ ràng và ghi nhớ các tính chất của đường tâm trong tam giác mà bạn đã chứng minh.

Bài tập áp dụng

Bài tập 1:

Trong tam giác ABC, M là trung điểm của cạnh BC. Chứng minh rằng đường trung bình AM chia đôi diện tích tam giác ABC.

Đáp án :

Ta biết rằng đường trung bình AM chia cạnh BC thành hai đoạn bằng nhau. Gọi H là giao điểm của AM và BH. Vì BH là đường cao của tam giác ABC, nên diện tích tam giác ABH bằng một nửa diện tích tam giác ABC. Tương tự, diện tích tam giác ACH cũng bằng một nửa diện tích tam giác ABC. Vì vậy, tổng diện tích tam giác ABH và tam giác ACH cũng bằng diện tích tam giác ABC. Nhưng ABH và ACH là hai tam giác đồng dạng (theo góc), nên diện tích của chúng cũng tỉ lệ bằng độ dài cạnh tương ứng. Do AM chia cạnh BC thành hai đoạn bằng nhau, nên diện tích tam giác ABH và tam giác ACH cũng bằng nhau. Vì vậy, đường trung bình AM chia đôi diện tích tam giác ABC.

Bài tập 2:

Trong tam giác ABC, M và N lần lượt là trung điểm của cạnh BC và cạnh AC. Chứng minh rằng đường trung bình AN cắt đường trung bình BM tại một điểm G, và AG = 2GN.

Đáp án :

Gọi G là điểm giao của đường trung bình AN và BM. Ta cần chứng minh rằng AG = 2GN.

Vì M là trung điểm của BC, ta có BM = MC. Đồng thời, N cũng là trung điểm của AC, nên AN = NC.

Theo định lí trung điểm, ta biết rằng G là trung điểm của AM và BN. Do đó, AG = GM và GN = NB.

Từ BM = MC và GN = NB, ta có BM + GN = MC + NB. Nhưng BM + GN = BG và MC + NB = BC.

Vậy BG = BC. Khi đó, theo định lí chia đôi, ta có AG = 2GN.

Vậy, chứng minh rằng đường trung bình AN cắt đường trung bình BM tại một điểm G, và AG = 2GN.

Bài tập 3:

Trong tam giác ABC, M là trung điểm của cạnh BC. Chứng minh rằng AM^2 = AB^2/2 + AC^2/2.

Đáp án:

Áp dụng định lý Pythagoras trong tam giác vuông ABM, ta có:

AM^2 = AB^2 + BM^2.

Vì M là trung điểm của BC, nên BM = MC = BC/2.

Thay BM = BC/2 vào công thức trên, ta có:

AM^2 = AB^2 + (BC/2)^2.

Mở rộng và đơn giản hóa công thức, ta được:

AM^2 = AB^2 + BC^2/4.

Nhưng theo định lý Pythagoras trong tam giác ABC, ta có:

BC^2 = AB^2 + AC^2.

Thay BC^2 = AB^2 + AC^2 vào công thức trên, ta có:

AM^2 = AB^2 + (AB^2 + AC^2)/4.

Tổng hợp các thành phần, ta có:

AM^2 = AB^2/2 + AC^2/2.

Vậy, chứng minh rằng AM^2 = AB^2/2 + AC^2/2.

Bài tập 4:

Trong tam giác ABC, M, N, P lần lượt là trung điểm của các cạnh BC, AC, AB. Chứng minh rằng đường trung bình AM, BN, CP cắt nhau tại một điểm duy nhất.

Đáp án:

Gọi G là điểm giao của đường trung bình AM và BN. Ta cần chứng minh rằng G cũng nằm trên đường trung bình CP.

Áp dụng định lí trung điểm, ta có GM = AM/2 và GN = BN/2.

Từ đó, ta có AG = AM - GM = AM - AM/2 = AM/2 và BG = BN - GN = BN - BN/2 = BN/2.

Vậy AG = BG.

Tương tự, ta áp dụng định lí trung điểm cho đường trung bình CP và AM, ta có CP = PM/2 và AP = AM - PM = AM - 2(PM/2) = AM - GM = AG.

Do đó, ta có AG = CP.

Vậy, G nằm trên đường trung bình CP.

Từ đó, ta kết luận rằng đường trung bình AM, BN, CP cắt nhau tại một điểm duy nhất, đó là điểm G.

Bài tập 5:

Trong tam giác ABC, M, N, P lần lượt là trung điểm của các cạnh BC, AC, AB. Chứng minh rằng tam giác MNP là tam giác đồng dạng với tam giác ABC.

Đáp án :

Gọi G là giao điểm của các đường trung bình AM, BN, CP.

Ta cần chứng minh rằng tam giác MNP đồng dạng với tam giác ABC, tức là tỉ lệ giữa các cạnh tương ứng là bằng nhau.

Áp dụng định lý trung điểm, ta có MG = AM/2, NG = BN/2 và PG = CP/2.

Từ đó, ta có tỉ lệ:

MN/AB = NG/BN = (BN/2)/(BN) = 1/2,

MP/AC = PG/CP = (CP/2)/(CP) = 1/2,

NP/BC = MG/AM = (AM/2)/(AM) = 1/2.

Vậy, ta có tỉ lệ giữa các cạnh tương ứng của tam giác MNP và tam giác ABC là bằng nhau.

Do đó, tam giác MNP đồng dạng với tam giác ABC.

Kết luận

Hy vọng rằng các bài tập này đã giúp bạn hiểu rõ hơn về tính chất và quan hệ giữa các đường trung bình trong tam giác. Đường trung bình không chỉ có vai trò trong việc phân chia độ dài cạnh mà còn có những tính chất đặc biệt khác như chia đôi diện tích, tạo ra các điểm giao đặc biệt, hay đồng dạng với tam giác gốc.