Định nghĩa tứ giác, phân loại tứ giác và công thức tính

Định nghĩa tứ giác là một khái niệm trong hình học Euclid, đề cập đến một hình học học bốn cạnh. Tứ giác được xác định bởi bốn điểm không thẳng hàng.

Trong lĩnh vực hình học, tứ giác là một thuật ngữ nổi tiếng và quan trọng. Tứ giác được xác định bởi bốn đỉnh không thẳng hàng và là hình cơ bản mà chúng ta thường gặp trong cuộc sống hàng ngày và trong các bài toán hình học. Từ hình chữ nhật và hình thoi cho đến những hình dạng bất thường hơn như hình vuông, hình tứ giác đóng một vai trò quan trọng trong việc nghiên cứu và phân tích các tính chất hình học của chúng.

Trong bài viết này của thayphu, chúng ta sẽ tìm hiểu định nghĩa tứ giác, các tính chất cơ bản và các điều kiện cần thiết để hình học bốn cạnh được coi là một tứ giác. Ngoài ra, chúng ta còn tìm hiểu về các loại tứ giác khác nhau và một số tính chất đáng chú ý của chúng.

Định nghĩa tứ giác được hiểu như thế nào?

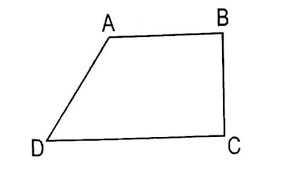
Định nghĩa tứ giác được hiểu như thế nào

Trong toán học, tứ giác là một đa giác có bốn cạnh và bốn đỉnh. Để được coi là một tứ giác, các đỉnh của nó phải là bốn điểm không thẳng hàng trong không gian hai chiều (mặt phẳng Euclide) hoặc trong không gian ba chiều (không gian Euclide ba chiều). Điều này có nghĩa là bốn điểm góc không nằm trên cùng một đường thẳng. Các cạnh của một tứ giác nối các đỉnh và tạo thành các đoạn thẳng. Một tứ giác có sáu cạnh (bốn cạnh và hai đường chéo) và bốn góc (các góc ở mỗi đỉnh).Góc ở mỗi đỉnh có thể được đo bằng đơn vị góc (thường là độ) và tổng các góc trong tứ giác là 360 độ.

Phân loại các tứ giác mà bạn nên biết

Dưới đây thayphu sẽ trình bày một số cách phân loại quan trọng của tứ giác mà bạn nên biết trong toán học và hình học:

Tứ giác lồi

Tất cả các góc của tứ giác lồi đều nhọn (các góc nhỏ hơn 180 độ). Tứ giác lồi là loại tứ giác phổ biến nhất và được nghiên cứu kỹ lưỡng trong hình học.

Tứ giác lõm

Tứ giác lõm là tứ giác có ít nhất một góc lõm (góc lớn hơn 180 độ).Trong một tứ giác lõm có ít nhất một đường chéo nằm ngoài tứ giác khi bị kéo dãn.

Tứ giác đều

Tứ giác đều là tứ giác có bốn cạnh và bốn góc bằng nhau.

Tứ giác vuông

Một trong bốn góc của tứ giác vuông là góc vuông (chính xác là 90 độ). Hai đường chéo của một hình vuông góc vuông có thể có độ dài khác nhau.

Tứ giác hình chữ nhật

Tứ giác hình chữ nhật là tứ giác có bốn góc vuông và các cạnh đối bằng nhau. Hai đường chéo của một tứ giác vuông có độ dài bằng nhau.

Tứ giác đều

Tứ giác đều có các cạnh bằng nhau và các góc tương ứng. Điều này có nghĩa là các cạnh đối diện và các góc đối diện trong một tứ giác bằng nhau có cùng độ dài và số lượng.

Tính chất của các loại tứ giác trong mặt phẳng

Dưới đây là một số tính chất của các loại tứ giác thường gặp trong mặt phẳng Euclide:

Tứ giác lồi

Tổng các góc trong một tứ giác lồi là 360 độ.

Các đường chéo cắt nhau tại một điểm trong tứ giác. Tổng độ dài của hai đường chéo bằng tổng độ dài của hai cặp cạnh đối diện.

Tứ giác lõm

Tổng các góc của một tứ giác lõm có thể lớn hơn 360 độ. Có ít nhất một đường chéo ở ngoài tứ giác khi mở rộng. - Tổng độ dài của hai đường chéo không nhất thiết phải bằng tổng độ dài của hai cặp cạnh đối diện.

Tứ giác đều

Các cạnh và các góc của một tứ giác đều có cùng chiều dài và kích thước.

Hai đường chéo bằng nhau và cắt nhau vuông góc.

Tổng các góc của một tứ giác là 360 độ.

Công thức để tính một tứ giác

Để tính một tứ giác, có một số công thức phụ thuộc vào loại tứ giác mà bạn đang xét. Dưới đây là một số công thức phổ biến:

Tứ giác bất kỳ

Để tính diện tích của một tứ giác bất kỳ, bạn có thể sử dụng công thức Heron:

Diện tích=√[s(s-a)(s-b)(s-c)],

Trong đó a, b, và c là độ dài các cạnh của tứ giác, và s là nửa chu vi được tính bằng công thức: s = (a + b + c) / 2.

Hình chữ nhật

Đối với hình chữ nhật, diện tích được tính bằng công thức:

Diện tích = chiều dài x chiều rộng.

Hình vuông

Đối với hình vuông, diện tích được tính bằng công thức:

Diện tích = cạnh x cạnh.

Hình thang

Đối với hình thang, diện tích được tính bằng công thức:

Diện tích = ((đáy lớn + đáy nhỏ) x chiều cao) / 2.

Hình tam giác

Đối với tam giác, có nhiều công thức tính diện tích, bao gồm:

Công thức Heron như đã trình bày ở trên.

Diện tích = 0.5 x cạnh x cạnh x sin(góc giữa 2 cạnh).

Phương pháp giải bài toán định nghĩa tứ giác

Để giải một bài toán liên quan đến định nghĩa tứ giác cần phải hiểu rõ yêu cầu của bài toán và các thông tin được cung cấp.

Dưới đây là phương pháp tổng quát để giải bài toán:

• Đọc và hiểu yêu cầu của bài toán: Đầu tiên, hãy đọc kỹ bài toán và hiểu yêu cầu của nó. Xác định loại hình tứ giác bạn đang xem xét (ví dụ: hình chữ nhật, hình vuông, hình thang, bất kỳ hình tứ giác nào, v.v.) và thông tin được cung cấp trong câu hỏi.
• Vẽ hình và gán biến: Vẽ hình tứ giác dựa vào thông tin cho trong bài. Gán các biến về độ dài cạnh và góc của tứ giác (nếu có). Hãy chắc chắn chú ý đến thông tin trên bản vẽ.
• Áp dụng công thức, quy tắc: Sử dụng các công thức, quy tắc liên quan đến loại tứ giác đang xét để giải bài toán. Điều này có thể bao gồm tính diện tích, chu vi, tìm góc trong tứ giác và các công thức liên quan khác.
• Giải phương trình (nếu cần): Trong một số trường hợp, có thể cần giải phương trình để tìm giá trị của biến trong bài toán.Sử dụng các công thức và quy tắc đã biết để thiết lập và giải phương trình để tìm giá trị mong muốn.
• Kiểm tra và trình bày kết quả: Sau khi tính toán kiểm tra kết quả và đảm bảo đúng. Nếu câu hỏi có yêu cầu, hãy trình bày kết quả rõ ràng, chính xác.

Cách vẽ một hình định nghĩa tứ giác

Để vẽ hình tứ giác các bạn có thể thực hiện theo các bước sau:

• Chuẩn bị dụng cụ vẽ: Các bạn cần chuẩn bị một tờ giấy, một cây bút chì, một cây bút mực và một thước kẻ.
• Xác định các đỉnh của tứ giác: Đọc yêu cầu bài tập hoặc thông tin về cách xác định các đỉnh của tứ giác. Ví dụ: đặt tên cho chúng là A, B, C và D.
• Vẽ các cạnh của hình vuông: Dùng thước kẻ và bút chì vẽ các đoạn thẳng nối các điểm góc lần lượt. Ví dụ: Vẽ các đoạn AB, BC, CD, DA để tạo thành một tứ giác. Đảm bảo đường bạn vẽ thẳng và không bị cong.
• Gán ký hiệu cho các đỉnh: Gán ký hiệu cho các đỉnh của hình vuông bằng cách viết các chữ cái tương ứng. Ví dụ: gán A cho đỉnh A, B cho đỉnh B, v.v.
• Đánh số độ dài các cạnh (tùy chọn): Nếu bài toán yêu cầu hoặc cung cấp thông tin về độ dài các cạnh thì có thể đánh số độ dài của chúng trên các đoạn thẳng tương ứng.Ví dụ: nếu AB = 5 cm, bạn có thể viết số 5 trên đoạn thẳng AB.
• Ghi thông tin bổ sung (tùy chọn): Nếu vấn đề yêu cầu hoặc cung cấp thêm thông tin thì ghi thông tin này vào kế hoạch. Ví dụ, nếu bài toán yêu cầu vẽ một hình chữ nhật, bạn có thể viết độ dài các cạnh hoặc góc vuông lên hình vẽ.
• Kiểm tra lại bản vẽ của bạn: Kiểm tra kỹ hình tứ giác bạn đã vẽ để đảm bảo các cạnh và đỉnh được vẽ chính xác và đáp ứng yêu cầu của bài toán.

Bài tập áp dụng

Bài tập 1: Định nghĩa tứ giác là gì? Liệt kê các yếu tố cần có để một hình góc đáp ứng định nghĩa tứ giác.

Đáp án:

Tứ giác là một hình học có bốn đỉnh và bốn cạnh. Để một hình góc được coi là tứ giác, cần có các yếu tố sau:

• Bốn đỉnh khác nhau không thẳng hàng.
• Bốn cạnh không có đỉnh chung.
• Bốn góc được tạo bởi các cạnh không trùng nhau.
• Bốn cạnh không nằm trên cùng một đường thẳng.

Bài tập 2: Cho một hình góc có bốn đỉnh A, B, C và D. Biết rằng AB = BC = CD và AD ≠ BD. Hãy xác định loại tứ giác mà hình góc đang đại diện và giải thích.

Đáp án: Hình góc đại diện cho một hình chữ nhật. Vì cả ba cạnh liên tiếp AB = BC = CD là bằng nhau, và hai đường chéo AD và BD không bằng nhau (AD ≠ BD). Điều này chỉ xảy ra trong hình chữ nhật, trong đó cả hai đường chéo không trùng nhau.

Bài tập 3: Phát biểu định nghĩa của một hình vuông. Liệt kê các đặc điểm đặc trưng của một hình vuông.

Đáp án: Hình vuông là một loại tứ giác có các đặc điểm sau:

• Có bốn cạnh bằng nhau.
• Có bốn góc vuông (góc 90 độ).
• Hai đường chéo cắt nhau vuông góc tại trung điểm của chúng.
• Có hai trục đối xứng: trục đối xứng qua các đường chéo và trục đối xứng qua các đường trung bình của cạnh.

Bài tập 4: Hãy trình bày định nghĩa của một tứ giác lồi và một tứ giác lõm. Đưa ra một ví dụ cụ thể cho mỗi loại tứ giác.

Đáp án:

• Tứ giác lồi: Là một tứ giác trong đó tất cả các đỉnh đều nằm trên cùng một phía của đường thẳng chứa cạnh nối hai đỉnh không liền kề. Ví dụ: hình chữ nhật, hình vuông.
• Tứ giác lõm: Là một tứ giác có ít nhất một đỉnh nằm trong phía bên trong của đường thẳng chứa cạnh nối hai đỉnh không liền kề. Ví dụ: hình thang, tứ giác không đều.

Bài tập 5: Cho một tứ giác ABCD với AB = AD, BC = CD và góc BAC = góc CDA = 90 độ. Hãy xác định loại tứ giác mà tứ giác ABCD đại diện và giải thích.

Đáp án :

Tứ giác ABCD đại diện cho một hình vuông. Vì cả hai cạnh liên tiếp AB = AD và BC = CD đều bằng nhau, và cả hai góc BAC và CDA đều là góc vuông (90 độ). Điều này chỉ xảy ra trong hình vuông.

Trên đây là một số thông tin của thayphu.net về định nghĩa tứ giác cùng với những bài tập tự luận. Hy vọng rằng những bài tập này đã giúp bạn hiểu rõ hơn về khái niệm và các loại tứ giác.Nếu bạn còn bất kì thắc mắc gì xin liên hệ với thayphu để được giải đáp nhé