Định lý thales là gì? Phân loại, hệ quả và bài tập áp dụng

Định lí Thales là một trong những định lí cơ bản trong hình học Euclid. Nó được đặt theo tên của nhà toán học Hy Lạp cổ Thales của Millet.

Định lý thales được định nghĩa như thế nào? Áp dụng sao cho hiệu quả

Trong lĩnh vực hình học Euclide, có một định lý mang tên Thales đã mê hoặc những người yêu toán học từ xa xưa. Định lý góc vuông thales đã đặt nền móng cho những khám phá về mối quan hệ giữa đường thẳng và đường tròn.Trong bài viết này của thayphu sẽ khám phá định lý này chi tiết hơn và tìm hiểu thêm về tầm quan trọng to lớn của nó đối với lĩnh vực hình học.

Định lý Thales còn được gọi là định lí gì trong toán học

Định lý Thales còn được gọi là định lí gì?

Định lý góc vuông thales đề cập đến mối quan hệ giữa đường thẳng và đường tròn. Người ta thường nói nếu có tam giác ABC có đỉnh A nằm trên đường tròn đường kính BC thì góc ABC là góc vuông

Điều này có nghĩa là đoạn thẳng nối đỉnh tam giác với tâm của tam giác tương ứng đường kính kết nối, tạo thành một góc vuông. Định lý Thales có thể được phát biểu Nếu một đường thẳng đi qua một đường tròn và tạo thành một tam giác thì góc giữa đường thẳng đó và đường kính của đường tròn đó bằng một góc vuông.Định lý này là một trong những nền tảng quan trọng trong việc xây dựng hình học Euclide và có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, trong đó có hình học phẳng và không gian.Cung cấp cách xác định góc vuông và xác định mối quan hệ hình học giữa các phần tử trong hình học tròn. Định lý góc vuông thales có ảnh hưởng sâu sắc đến sự phát triển của hình học và toán học nói chung. Nó không chỉ giúp chúng ta hiểu các quy luật cơ bản của hình học mà còn là bàn đạp quan trọng cho những khám phá và định lý hình học phức tạp hơn trong tương lai.

Tính chất của một định lý góc vuông Thales mà bạn nên biết

Định lý có một số tính chất quan trọng:

Góc vuông

Định lý phát biểu rằng góc ABC là góc vuông. Điều này có nghĩa là góc giữa đường thẳng đi qua đỉnh A và đường kính BC của đường tròn tương ứng là góc vuông có kích thước 90 độ.

Góc phụ

Định lý góc vuông Thales còn có một tính chất quan trọng khác liên quan đến các góc bổ sung.Nếu có một đường thẳng khác đi qua đỉnh A và cắt đường tròn tại điểm B khác thì góc ABD tạo thành cũng là góc vuông. Điều này có nghĩa là góc giữa đường thẳng đi qua đỉnh A và đường kính của đường tròn tại giao điểm khác cũng là góc vuông.

Đường kính

Định lý góc vuông phát biểu rằng đường kính BC của hình tròn là một cạnh của tam giác ABC. Điều này chứng tỏ đường thẳng BC là đường chéo của tam giác ABC.

Tính tỉ lệ của độ dài

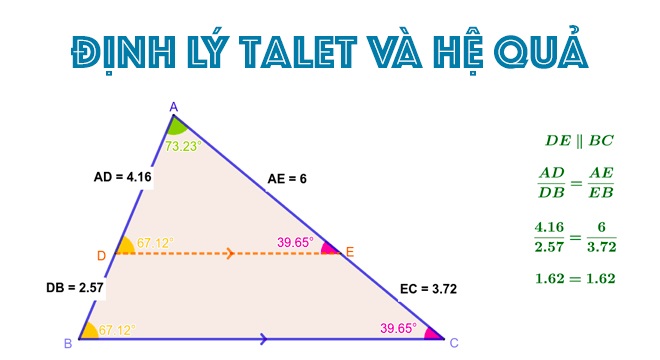
Một tính chất thú vị khác của định lý góc vuông là tính tỉ lệ của độ dài. Nếu vẽ một đường thẳng song song với đường kính BC và cắt các cạnh AB, AC lần lượt tại các điểm D và E thì độ dài các đoạn AD, DE và EC tỉ lệ thuận với nhau. Nói cách khác: AD/DB = DE/EC.

Tính đối xứng

Định lý này cũng có tính đối xứng. Nghĩa là, nếu một đường thẳng đi qua đỉnh A và cắt đường tròn tại hai điểm B và C thì đường thẳng đối diện đi qua đỉnh A và cắt đường tròn tại hai điểm khác D và E thì BD/DC = BE/EA

Điều này có nghĩa là tỉ số giữa khoảng cách trên cạnh ABC của tam giác và khoảng cách trên cạnh ADE của tam giác là như nhau.

Phân loại các định lý góc vuông Thales trong một tam giác

Trong một tam giác có một số định lý quan trọng của Thales về góc vuông. Dưới đây là định lý góc vuông của Thales, phân loại theo các trường hợp khác nhau:

• Định lý góc vuông của Thales:Định lý này phát biểu rằng nếu có tam giác ABC có đỉnh A nằm trên đường tròn đường kính BC thì góc ABC ( góc ở đỉnh A) là góc vuông.
• Định lý nghịch đảo góc vuông Thales (Định lý ngược): Định lý này phát biểu rằng nếu góc ABC (góc tại đỉnh A) là góc vuông thì đỉnh A nằm trên đường tròn đường kính BC.
• Định lý góc vuông mở rộng của Thales: Định lý này áp dụng khi một đường thẳng đi qua một đỉnh của một tam giác và cắt đường tròn tại hai điểm phân biệt. Nếu đoạn thẳng chứa cạnh của tam giác cắt đường tròn tại một điểm và cạnh kia cắt đường tròn tại một điểm khác thì góc ở đỉnh đó là góc vuông.
• Định lý góc vuông mở rộng ngược của Thales (định lý nghịch đảo): Định lý này áp dụng nếu góc ở đỉnh của tam giác vuông.Nếu đoạn thẳng chứa cạnh của tam giác cắt đường tròn tại một điểm và cạnh kia cắt đường tròn tại một điểm khác thì đoạn thẳng chứa cạnh cắt đường tròn tại điểm thứ hai.

Quy tắc của định lý góc vuông Thales trong hình học

Định lý góc vuông của Thales phát biểu rằng nếu một đỉnh của một tam giác nằm trên một đường tròn có đường kính là cạnh đối diện với góc vuông thì góc ở đỉnh đó là góc vuông.

Để sử dụng định lý này trong tính toán, chúng ta không cần một công thức đặc biệt nào, chúng ta chỉ cần biết rằng nếu một đỉnh của tam giác nằm trên một đường tròn có đường kính là cạnh đối diện với bên phải thì ta có thể kết luận rằng góc đó bằng ở góc là đỉnh này nó là một góc vuông.

Ví dụ: Nếu chúng ta có tam giác ABC có BC là cạnh đối diện với góc vuông tại đỉnh A. Nếu biết đỉnh A nằm trên đường tròn đường kính BC thì ta có thể kết luận góc ABC (góc ở đỉnh A) là góc vuông.

Chứng minh định lý góc vuông Thales mà bạn đã biết

Để chứng minh định lý góc vuông của Thales, chúng ta cần sử dụng một số khái niệm, định lý hình học cơ bản. Đây là một cách chứng minh định lý góc vuông của Thales:

Giả sử chúng ta có tam giác ABC có đỉnh A nằm trên đường tròn đường kính BC. Ta cần chứng minh góc ABC là góc vuông.

• Bước 1: Vẽ hình và khám phá các yếu tố hình học.Vẽ tam giác ABC và đường tròn đường kính BC.Ta cần chứng minh góc ABC là góc vuông.
• Bước 2: Xét tam giác vuông BAC. Vì đường tròn có đường kính BC nên góc BAC nội tiếp trên cung BC.
• Bước 3: Sử dụng nguyên lý trong hình học tam giác. Định lý này phát biểu rằng tổng các góc của một tam giác là 180 độ.
• Bước 4: Xét tam giác BAC. Tổng các góc của tam giác BAC là A + B + C = 180 độ. Bước 5: Vì tam giác BAC là tam giác vuông nên góc BAC là góc vuông.

Vậy A + B + C = 180 độ có thể viết lại thành A + B + 90 độ = 180 độ.

• Bước 6: Loại bỏ góc BAC hai vế của phương trình trên. Chúng ta có A + B = 90 độ. Bước 7: Kết luận góc ABC là góc vuông. Vì A + B = 90 độ nên góc ABC là góc vuông. Với các bước chứng minh trên ta đã chứng minh được góc ABC là góc vuông theo định lý góc vuông của Thales.

Cách phân biệt định lý cơ bản và định lý ngược trong góc vuông Thales

Định lý góc vuông cơ bản của Thales và định lý góc vuông nghịch đảo của Thales (ngược lại) là hai khía cạnh đối lập nhau trong định lý này. Sau đây là cách phân biệt hai định lý này:

Định lý góc vuông cơ bản Thales: Định lý này phát biểu rằng nếu tam giác ABC có đỉnh A nằm trên đường tròn đường kính BC thì góc ABC (góc ở đỉnh A) giữ nguyên) là một góc vuông.Đây là một phát biểu tổng quát và thường gặp trong hình học tam giác và cho phép chúng ta kết luận rằng một góc là đúng nếu chúng ta biết rằng cạnh đối diện nằm trên đường tròn.

Định lý nghịch đảo góc vuông Thales: Định lý này phát biểu rằng nếu góc ABC (góc ở đỉnh A) là góc vuông thì đỉnh A nằm trên đường tròn đường kính BC. Định lý này cho phép làm điều ngược lại: nếu biết một góc là góc vuông thì ta có thể kết luận rằng đỉnh của góc đó nằm trong một đường tròn có đường kính cạnh đối diện.

Những phương pháp để giải bài toán về định lí góc vuông Thales

Để giải các bài toán liên quan đến định lý góc vuông của Thales, bạn có thể sử dụng nhiều phương pháp và kỹ thuật khác nhau. Dưới đây là một số phương pháp phổ biến:

Vẽ hình

Đầu tiên vẽ hình theo yêu cầu của bài toán và đảm bảo các phần tử có liên quan đến định lý góc vuông trong hình tam giác, các cạnh, các đỉnh và các vòng tròn được hiển thị rõ ràng trong bản vẽ.

Sử dụng công thức tính góc trong tam giác: Áp dụng công thức tính góc trong tam giác,ví dụ: tổng các góc trong một tam giác bằng 180 độ, công thức góc nội tiếp hoặc công thức góc ngoại tiếp để tìm mối quan hệ giữa góc trong và góc vuông của tam giác.

Sử dụng công thức đường tròn

Nếu bài toán có liên quan đến đường tròn và góc Thales vuông thì sử dụng các công thức đường tròn như đường kính, bán kính, cung để xác định mối liên hệ giữa các phần tử của bài toán.

Sử dụng chứng minh hình học

Trong một số trường hợp, bạn có thể sử dụng phương pháp chứng minh hình học để chứng minh các phát biểu và mối quan hệ liên quan đến định lý góc vuông của Thales.

Bài tập áp dụng

Bài tập 1:

Cho một tam giác ABC có đỉnh A nằm trên đường tròn có đường kính BC. Chứng minh rằng góc ABC là góc vuông.

Đáp án:

Ta có thể sử dụng cách chứng minh đã trình bày ở phần trước để chứng minh rằng góc ABC là góc vuông.

Bài tập 2:

Hình bên là một đường tròn có đường kính AB. Điểm C nằm trên đoạn thẳng AB sao cho AC = 2CB. Chứng minh rằng góc ACB là góc vuông.

Đáp án:

Gọi O là tâm của đường tròn. Vì AC = 2CB, ta có AO = AC + CO = 2CB + CO = 2CO + CO = 3CO. Do đó, tam giác AOC là tam giác vuông và góc AOC là góc vuông. Vì góc ACB là góc nội tiếp cùng cung với góc AOC, nên góc ACB cũng là góc vuông.

Bài tập 3:

Trong một tứ giác ABCD nội tiếp đường tròn, các đường chéo AC và BD cắt nhau tại điểm E. Chứng minh rằng tam giác AEB và tam giác CED là tam giác đồng dạng.

Đáp án:

Gọi O là tâm của đường tròn. Ta có góc AOB là góc vuông (do định lí Thales). Tương tự, ta cũng có góc COD là góc vuông. Do đó, tam giác AOB và tam giác COD là hai tam giác vuông. Vì hai tam giác này có một góc chung và một góc vuông chung, nên chúng là tam giác đồng dạng theo trường hợp góc-góc-góc.

Bài tập 4:

Trong một tam giác ABC vuông tại A, đường cao AH cắt đường tròn ngoại tiếp tam giác ABC tại điểm H. Chứng minh rằng góc BHC là góc vuông.

Đáp án:

Vì AH là đường cao của tam giác ABC, nên góc BAH và góc CAH là góc vuông. Vì đường tròn ngoại tiếp tam giác ABC cắt đường cao AH tại điểm H, nên góc BHC và góc BAC là cùng góc nội tiếp cùng cung. Vì vậy, góc BHC cũng là góc vuông.

Bài tập 5:

Trong một tứ giác ABCD nội tiếp đường tròn, gọi M và N lần lượt là trung điểm của AC và BD. Chứng minh rằng MN vuông góc với AB.

Đáp án:

Gọi O là tâm của đường tròn. Ta có MO song song với AC và NO song song với BD (do trung điểm của cạnh song song với đỉnh tạo thành đường chéo). Vì vậy, MO và NO vuông góc với AB. Do đó, MN cũng vuông góc với AB vì là đường thẳng nối hai điểm vuông góc với cùng một đường thẳng.

Kết luận

Trên đây là cách chứng minh và một số bài tập liên quan đến định lí Thales. Định lí này là một trong những định lí cơ bản trong hình học và có ứng dụng rộng trong các bài toán liên quan đến đường tròn và tam giác. Việc hiểu và áp dụng định lí này sẽ giúp chúng ta nắm bắt và giải quyết các bài toán hình học một cách chính xác.