Định lý Pythagore, cách chứng minh và các bài tập vận dụng

Định lý Pythagore phát biểu như thế nào? Cách chứng minh định lý và ứng dụng của định lý Pythagore kèm các bài tập vận dụng cực hay.

Định lý Pythagore là một trong những định lý cơ bản và quan trọng nhất trong hình học Euclid. Nó được đặt theo tên của nhà toán học Hy Lạp cổ Pythagoras. Đây là định lý cơ bản và nền tảng của chương trình toán lớp 7, bởi nó liên quan đến mối quan hệ giữa độ dài của các cạnh trong tam giác vuông.

Vì vậy trong bài viết này, hãy vùng thayphu tìm hiểu các kiến thức về định lý Pitago như khái niệm, cách chứng minh và các bài tập vận dụng của nó nhé.

Định lý pythagore

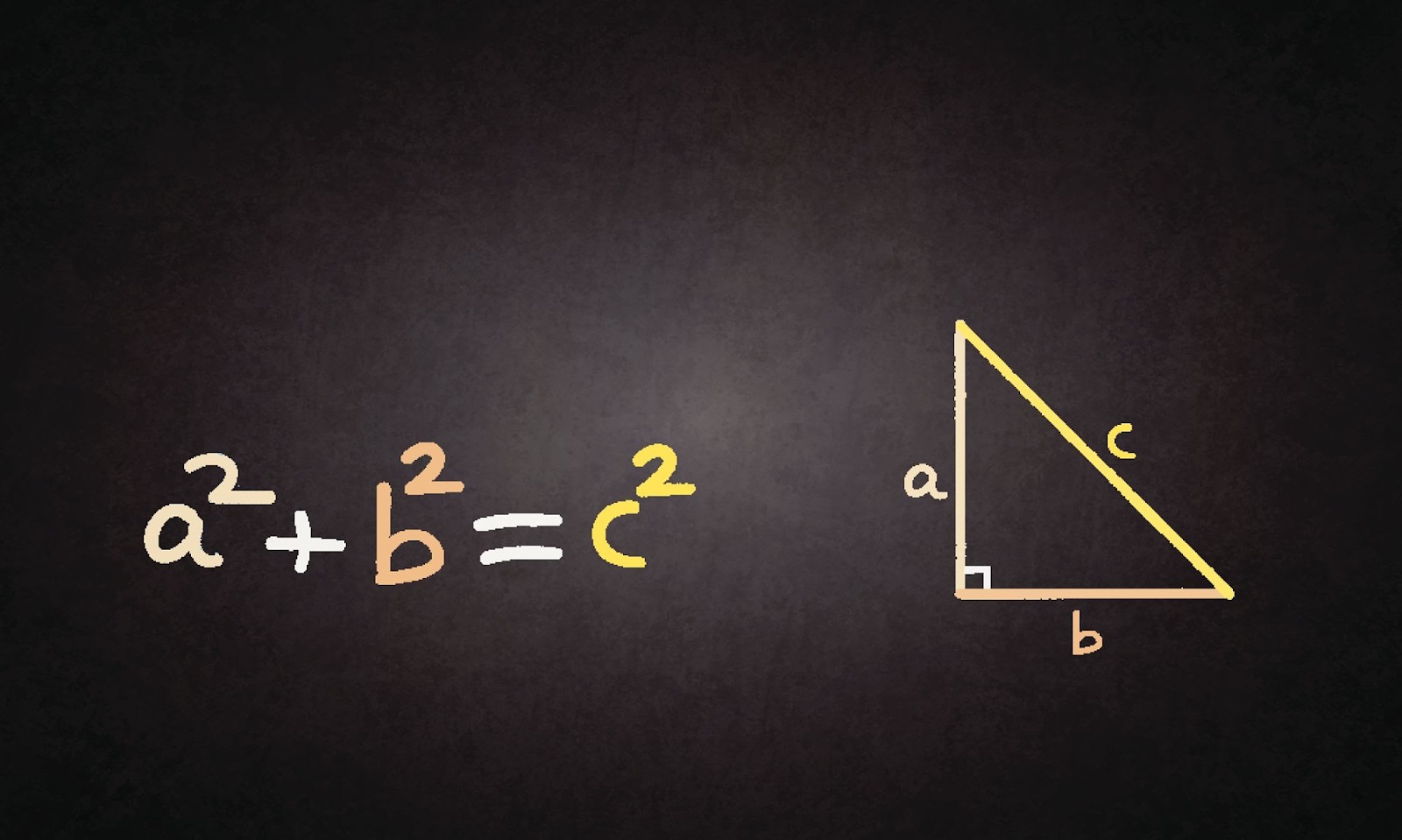
Định lý Pythagore (Pythagoras hay Pytago) là định lý về mối quan hệ giữa độ dài của các cạnh trong tam giác vuông.

Định lý Pythagore thuận phát biểu như sau: “Trong một tam giác vuông, bình phương độ dài cạnh huyền (cạnh đối diện góc vuông) bằng tổng bình phương độ dài hai cạnh góc vuông”.

Định lý Pythagore có công thức tổng quát như sau:

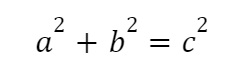
Trong đó:

c: độ dài cạnh huyền của tam giác vuông

a, b: lần lượt là độ dài của hai cạnh góc vuông

Ví dụ: Trong tam giác ABC, có góc A = 90°. AB = 3, AC = 4. Tính độ dài đoạn thẳng BC.

Từ định lý Pytago, ta suy ra:

AB^2 + AC^2 = BC^2

⇔ BC^2 = 3^2 + 4^2 = 9 + 16 = 25

⇒ BC =5

Định lý pythagore đảo

Định lý Pythagore đảo, còn được gọi là Định lý Pythagore ngược. Nó được phát biểu như sau: “Nếu trong một tam giác, bình phương độ dài cạnh lớn nhất bằng tổng bình phương độ dài hai cạnh còn lại, thì tam giác đó là tam giác vuông.”

Định lý Pythagore đảo có công thức như sau:

Nếu a, b, c là độ dài của ba cạnh của một tam giác và c là cạnh lớn nhất (huyền) và nếu:

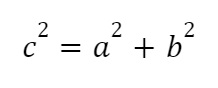
thì tam giác này là tam giác vuông.

Ví dụ: Tam giác ABC, có AB = 6, AC = 8, BC = 10. Thì ta có thể suy ra tam giác ABC là tam giác vuông do 6^2 + 8^2 = 10^2 hay AB^2 + AC^2 = BC^2.

Định lý Pytago đảo có một hệ quả đó là cách xác định đơn giản một tam giác là tam giác vuông, hay tam giác nhọn hoặc tam giác tù. Gọi c là cạnh dài nhất của tam giác và a + b > c. Ta có các phát biểu như sau:

• Nếu a^2 + b^2 = c^2, thì tam giác vuông.
• Nếu a^2 + b^2 > c^2, thì tam giác nhọn.
• Nếu a^2 + b^2 < c^2, thì tam giác tù.

Cách chứng minh định lý Pythagore

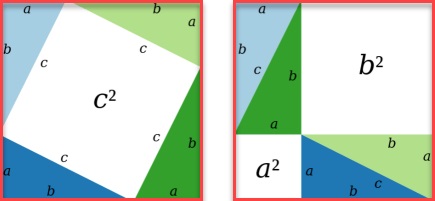
Nhà toán học Pythagore đã chứng minh định lý của mình thông qua hình minh họa như trên.

Ở hình minh họa như trên, ta có 2 hình vuông lớn và chúng đều có diện tích bằng nhau là: (a+b)^2

Ở mỗi hình cũng đều có 4 tam giác vuông bằng nhau và diện tích bằng nhau là 1/2(a.b). Tuy nhiên, sự khác nhau giữa hai hình vuông trên là các sắp xếp các tam giác vuông khác nhau. Từ đó, có thể thấy diện tích khoảng trắng của cả 2 hình sẽ bằng nhau.

Ta có thể kết luận, diện tích của hình vuông c bình phương sẽ bằng tổng diện tích của 2 hình vuông a bình và b bình nên ta có rút ra kết luận về định lý của Pythagore:

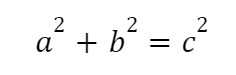
Ứng dụng của định lý Pythagore trong cuộc sống

Định lý Pythagore được coi là một trong 17 phương trình giải cứu thế giới. Bởi nó có rất nhiều ứng dụng trong nhiều lĩnh vực khác nhau. Trong bài viết này thayphu sẽ liệt kê 1 vài ứng dụng nổi bật của nó như:

• Hình học không gian: Như ta đã biết, định lý Pytago được sử dụng để tính toán độ dài đường chéo của các hình hộp chữ nhật, hình cầu, hình trụ và nhiều hình dạng khác. Từ đó ta có thể tính được diện tích, thể tích và khoảng cách trong không gian.
• Thiết kế và kiến trúc: Đây được coi là công cụ quan trọng trong thiết kế và kiến trúc. Công thức này giúp xác định kích thước và vị trí chính xác của các thành phần trong các công trình xây dựng.
• Đo đạc và định vị: Định lý này cũng được sử dụng trong các ứng dụng đo đạc và định vị. Ví dụ, trong đo đạc địa hình, nó có thể được sử dụng để tính toán khoảng cách giữa hai điểm dựa trên tọa độ của chúng. Ngoài ra, trong định vị GPS, định lý Pythagore có thể được áp dụng để tính toán vị trí dựa trên tọa độ đo được.
• Vật lý: Trong lĩnh vực vật lý, Định lý Pythagore được sử dụng để tính toán các đại lượng như vận tốc, gia tốc và lực. Nó cung cấp cơ sở cho các phương trình và mô hình vật lý trong nhiều lĩnh vực khác nhau, từ cơ học đến quang học và hạt nhân.

Bài tập vận dụng tự ôn tập

Bài tập 1: Cho tam giác ABC vuông tại đỉnh A. Biết cạnh BC = 15 và AB = 2AC. Hãy tính độ dài cạnh AB và AC.

Gợi ý lời giải:

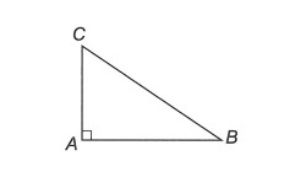
Áp dụng định lý Pytago, ta có AB^2 + AC^2 = BC^2.

Biết BC = 15 và AB = 2AC ⇒ (2AC)^2 + AC^2 = 15^2

⇔ 5AC^2 =225

⇔ AC^2 = 45 ⇒ AC = √45.

⇔ AB = 2√45

Vậy độ dài cạnh AB = 2√45 và AC = √45.

Bài tập 2: Cho tam giác ABC, có đường cao AH, điểm H thuộc đoạn BC như hình minh họa sau. Hãy tính giá trị của x.

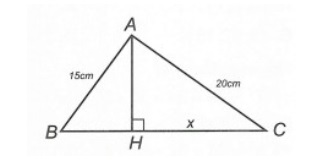
Gợi ý lời giải:

Áp dụng định lý Pitago trong tam giác vuông:

Xét tam giác ABC vuông tại A, ta có thể suy ra độ dài đoạn BC

BC = √(AB^2 + AC^2) = √(15^2 + 20^2) = 25

⇒ BH = BC - HC = 25 - x

Xét tam giác ABH vuông tại H và ACH vuông tại H:

AB^2 = AH^2 + BH^2, AC^2 = AH^2 + HC^2

⇒ AB^2 - BH^2 = AC^2 - HC^2 = AH^2

⇔ 15^2 - (25 - x)^2 = 20^2 - x^2

⇔ x = 16

Vậy giá trị cần tìm của x = 16.

Bài tập 3: Tam giác ABC vuông tại A, biết BC = 26, AC = 10. Hãy tính chu vi của tam giác ABC.

Gợi ý lời giải:

Áp dụng định lý Pitago trong tam giác ABC, ta có:

AB^2 + AC^2 = BC^2

⇔ AB^2 = BC^2 - AC^2

⇔ AB^2 = 26^2 - 10^2 = 576

⇒ AB = 24

Vậy chu vi tam giác ABC = 24 + 26 + 10 = 60.

Kết luận

Qua bài viết trên, thayphu hy vọng rằng các bạn đã nắm rõ các kiến thức về định lý Pythagore. Đây là một khía cạnh quan trọng trong hình học và toán học, bởi nó có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Vì vậy mà chúng ta cần hiểu và áp dụng định lý này thật tốt để giúp chúng ta giải các dạng toán từ cơ bản đến nâng của của định lý Pitago nhé.