Diện tích hình vuông, tổng hợp công thức và cách tính chuẩn

Diện tích hình vuông là một giá trị số đo diện tích của một hình vuông. Nó thể hiện tổng diện tích của tất cả các mặt phẳng bên trong hình vuông.

Diện tích hình vuông không chỉ là một khái niệm trừu tượng mà còn gắn liền với nhiều lĩnh vực của đời sống hàng ngày. Từ kiến trúc đến quy hoạch đô thị, từ kinh tế đến công nghệ, diện tích hình vuông đóng vai trò quan trọng trong việc đo lường,tính toán.Trong bài viết này của thayphu chúng ta hãy cùng nhau khám phá diện tích hình vuông, từ công thức tính cơ bản đến ứng dụng thực tế của nó.

Diện tích hình vuông là gì?

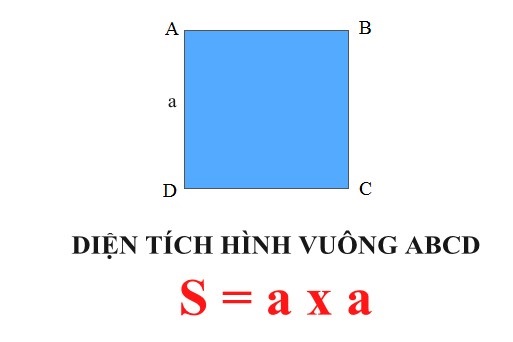
Diện tích hình vuông được hiểu như thế nào

Diện tích của hình vuông là khái niệm đo diện tích của hình vuông. Xác định tổng số đơn vị diện tích mà hình vuông chiếm giữ trên mặt phẳng.

Để hiểu cách tính diện tích của hình vuông, chúng ta cần biết hình vuông có các cạnh bằng nhau và các góc vuông (góc 90 độ). Nếu biết độ dài một cạnh của hình vuông, chúng ta có thể tính diện tích bằng cách nhân độ dài cạnh đó với chính nó.

Tính chất của diện tích một hình vuông

Diện tích một hình vuông có một số tính chất quan trọng:

Tính đối xứng

Diện tích hình vuông không thay đổi nếu chúng ta xoay hình vuông qua một góc bất kỳ. Điều này có nghĩa là nếu chúng ta xoay hình vuông 180 độ thì diện tích vẫn giữ nguyên.

Nhân đôi

Nếu ta nhân đôi chiều dài cạnh của hình vuông thì diện tích cũng tăng gấp đôi.Ví dụ: nếu chúng ta có hình vuông có cạnh dài a thì diện tích là a^2. Nếu chúng ta tăng độ dài cạnh lên 2a thì diện tích là (2a)^2 = 4a^2, gấp đôi diện tích ban đầu.

Hình tròn

Diện tích của hình vuông không thay đổi nếu chúng ta di chuyển nó quanh một mặt phẳng mà hình dạng của nó không thay đổi. Nghĩa là, nếu chúng ta di chuyển hình vuông từ vị trí này sang vị trí khác trong mặt phẳng mà không thay đổi cạnh hoặc góc thì diện tích vẫn giữ nguyên

Không âm

Diện tích của hình vuông luôn có giá trị không âm, có thể bằng 0 hoặc dương. Tuy nhiên, diện tích không thể là một giá trị âm.

Đối xứng cạnh nhau

Diện tích của hình vuông không thay đổi nếu ta lấy độ dài cạnh đó làm trục đối xứng và lật hình vuông về cạnh đó.Điều này có nghĩa là nếu chúng ta lấy hình vuông ban đầu và lật nó lại thì diện tích vẫn giữ nguyên.

Các ông thức tính diện tích hình vuông trong toán học

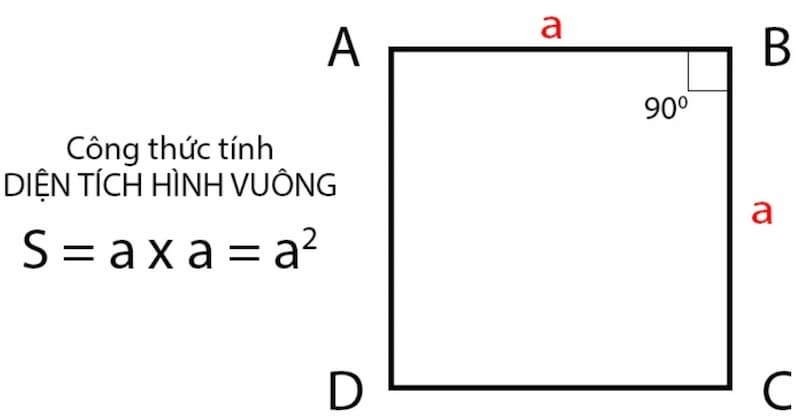
Tổng hợp công thức tính diện tích một hình vuông

Công thức tính diện tích một hình vuông rất đơn giản. Diện tích được tính bằng cách nhân độ dài một cạnh của hình vuông với chính nó.

Nếu độ dài cạnh của hình vuông là a thì công thức tính diện tích là:

Diện tích = a x a = a^2

Sử dụng công thức trên, ta nhân độ dài cạnh với chính nó để tính diện tích và Kết quả đó tính bằng đơn vị vuông (ví dụ: mét vuông, cm vuông, feet vuông, v.v.).

Ví dụ: Nếu chúng ta có một hình vuông có mỗi cạnh 4 mét, chúng ta có thể tính diện tích bằng cách nhân 4 với chính nó:

Diện tích = 4 x 4 = 16 mét vuông.

Một số công thức tính diện tích hình vuông khác

Công thức tính diện tích một hình vuông lớp 3

Trong môn toán lớp 3, diện tích một hình vuông được tính bằng cách nhân độ dài một cạnh với chính nó. Giả sử độ dài cạnh của hình vuông là a.

Do đó, công thức tính diện tích một hình vuông trong toán lớp 3 là:

Diện tích = a x a = a^2

Công thức tính diện tích hình vuông lớp 4

Toán lớp 4 vẫn sử dụng công thức cơ bản như các lớp trước để tính diện tích hình vuông. Điều này có nghĩa là nhân chiều dài một cạnh của hình vuông với chính nó.

Giả sử độ dài cạnh của hình vuông là a, công thức tính diện tích hình vuông là:

Diện tích = a x a = a^2

Ví dụ: Nếu bạn có một hình vuông có cạnh là dài 5 cm, Bạn có thể tính diện tích bằng cách nhân 5 với chính nó:

Diện tích = 5 cm x 5 cm = 25 cm²

Vì vậy, công thức tính diện tích một hình vuông trong toán lớp 4 vẫn là nhân và chỉ tính chiều dài của cạnh và kết quả được hiển thị theo đơn vị vuông (ví dụ: cm2, m2, v.v.).

Công thức tính diện tích một hình vuông lớp 5

Ở môn toán lớp 5, công thức tính diện tích một hình vuông không thay đổi so với các lớp trước. Vẫn nhân chiều dài một cạnh hình vuông với chính nó.

Giả sử chiều dài cạnh hình vuông là a thì công thức tính diện tích hình vuông là:

Diện tích = a x a = a^ 2

Ví dụ: Nếu bạn có một hình vuông có cạnh dài 6 cm, bạn có thể tính diện tích bằng cách nhân 6 với chính nó:

Diện tích = 6 cm x 6 cm = 36 cm²

Do đó, công thức tính diện tích một diện tích là một Hình vuông trong toán lớp 5 vẫn liên quan đến việc nhân chiều dài của cạnh được tính và kết quả được hiển thị theo đơn vị hình vuông (ví dụ: cm2, m2, v.v.).

Công thức nâng cao để tính diện tích một hình vuông

Để tính diện tích của một hình vuông mở rộng, ngoài việc đơn giản là nhân độ dài cạnh với chính nó, chúng ta còn có thể sử dụng một số công thức phụ thuộc vào những thông tin khác về hình vuông.

Dưới đây là một số công thức nâng cao để tính diện tích hình vuông:

Sử dụng đường chéo

Nếu biết độ dài đường chéo của hình vuông, chúng ta có thể tính diện tích bằng công thức:

Diện tích = (Chiều dài đường chéo ) ^2 / 2

Sử dụng bán kính hình tròn xung quanh

Nếu biết bán kính hình tròn xung quanh hình vuông thì ta có thể tính diện tích bằng công thức:

Diện tích = 2 x (Bán kính)^2

Sử dụng chu vi

Nếu biết chu vi hình vuông, chúng ta có thể tính diện tích bằng công thức:

Diện tích = (Chu vi)^2 / 16

Với góc nội tiếp

Nếu biết góc nội tiếp của hình vuông, ta có thể tính diện tích bằng công thức:

Diện tích = (cạnh)^2 x sin(góc)

Chứng minh diện tích một hình vuông

Để chứng minh diện tích một hình vuông chúng ta có thể sử dụng phương pháp hình học hoặc đại số. Đây là một bằng chứng hình học đơn giản: Giả sử chúng ta có một hình vuông có cạnh dài là a. Để tính diện tích một hình vuông, chúng ta cần tìm diện tích của hình bao quanh nó.

• Bước 1: Vẽ hình vuông và đánh dấu độ dài cạnh là a.
• Bước 2: Vẽ đường thẳng từ một đỉnh của hình vuông đến đỉnh đối diện.Đường thẳng này chia hình vuông thành hai hình tam giác đều.
• Bước 3: Vẽ một đường thẳng khác từ một đỉnh khác của hình vuông đến đỉnh đối diện. Đường thẳng này chia hình vuông thành hai hình tam giác đều hơn.
• Bước 4: Ta để ý các đường thẳng vẽ tạo thành hình chữ nhật bao quanh hình vuông ban đầu.
• Bước 5: Chiều dài một cạnh của hình chữ nhật là a nhưng chiều dài cạnh kia là 2a vì ta chia hình vuông thành hai hình tam giác đều.Do đó,diện tích hình chữ nhật là a x 2a = 2a^2.
• Bước 6: Tuy nhiên chúng ta chỉ quan tâm đến diện tích một hình vuông ban đầu. Vì hình vuông ban đầu chiếm một nửa diện tích hình chữ nhật xung quanh nên ta chia diện tích hình chữ nhật cho 2.

Kết quả là diện tích hình vuông ban đầu là (2a^2)/2 = a^ 2, nghĩa là diện tích bằng a nhân với chính nó.

Chứng minh trên cho thấy diện tích một hình vuông là a^2, từ đó thể hiện công thức tính diện tích một hình vuông.

Một số lưu ý khi giải bài tập diện tích hình vuông

Khi giải bài toán hình vuông cần chú ý các điểm quan trọng sau:

• Xác định các phân tích đơn vị: Hãy chắc chắn rằng các phân tích đơn vị đã biết cần có trong bài toán để có thể tính toán kết quả đúng. Ví dụ: mét vuông, centimet vuông, foot vuông, vv
• Đọc và hiểu câu hỏi: Vui lòng đọc kỹ câu hỏi để hiểu rõ yêu cầu và thông tin được cung cấp. Xác định những gì cần tính toán và đảm bảo bạn hiểu các điều khoản và giả định của mục đó.
• Xác định giá trị cạnh: Xác định giá trị cạnh vuông dựa vào thông tin hoặc điều kiện cho trong bài. Nếu không biết giá trị của cạnh, bạn có thể giả sử đó là a và tiếp tục tính toán. Sử dụng công thức tính diện tích: Sử dụng công thức tính diện tích hình vuông (Diện tích = Cạnh x Cạnh hoặc Diện tích = Cạnh^2) để tính diện tích. Áp dụng công thức đúng và đảm bảo bạn sử dụng đúng giá trị.
• Kiểm tra kết quả: Sau khi tính tích, kiểm tra kết quả để đảm bảo tính đúng.Đánh giá xem kết quả có phù hợp và có thể kiểm tra bằng các phương pháp khác hay không. Trình bày kết quả: Trình bày kết quả cuối cùng theo đơn vị diện tích yêu cầu và trình bày rõ ràng, dễ hiểu.

Khi giải bài toán tính diện tích hình vuông, những mẹo mà thayphu.net đã đưa đến cho bạn sẽ giúp bạn tiếp cận bài toán một cách cẩn thận và chính xác. Bằng cách đọc và hiểu bài toán, xác định giá trị cạnh, sử dụng công thức tính diện tích và kiểm tra kết quả, các em sẽ dễ dàng giải được các bài toán liên quan đến diện tích hình vuông. Luôn trình bày kết quả rõ ràng và đảm bảo yêu cầu đúng đơn vị diện tích. Với việc thực hành và nâng cao kỹ năng của mình, bạn sẽ trở thành người giải thành thạo các bài toán diện tích bậc hai.