Tính diện tích hình thoi, tổng hợp đầy đủ kèm bài tập áp dụng

Diện tích hình thoi là một khái niệm trong hình học, đo lường diện tích của một hình thoi.Hãy cùng chúng tôi tìm hiểu cách tính diện tích hình thoi nhé.

Trong lĩnh vực hình học, diện tích là một khái niệm quan trọng giúp chúng ta đo và tính diện tích theo nhiều cách khác nhau. Trong bài viết này của thayphu, chúng ta sẽ tìm hiểu về diện tích hình thoi và những khía cạnh xung quanh chúng.

Hình thoi hay còn gọi là hình gì trong toán học

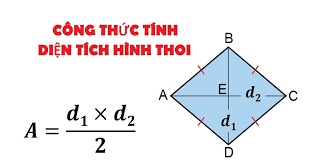
Hình thoi hay còn gọi là hình gì trong toán học

Trong toán học, hình thoi là một dạng hình học đặc biệt với những tính chất độc đáo. Hình thoi được định nghĩa là một hình vuông có các cạnh được kéo dài hoặc thu hẹp sao cho cạnh trái và cạnh phải không song song. Điều này có nghĩa là bốn cạnh của hình thoi có chiều dài bằng nhau và hai góc đối diện bằng nhau.

Hình thoi có nhiều ứng dụng trong toán học và thực tế. Ví dụ, trong hình học, diện tích hình thoi có thể được tính bằng cách nhân độ dài các cạnh đối diện của hình thoi và chia kết quả cho một nửa. Hình thoi cũng thường xuất hiện trong các vấn đề về tính tỷ lệ và tính đối xứng.

Tóm lại, hình thoi là hình vuông có các cạnh không song song và các góc đối diện bằng nhau.Đây là một khái niệm cơ bản trong toán học và có nhiều ứng dụng thực tế.

Tổng hợp các công thức tính diện tích hình thoi

Dưới đây thayphu đã tổng hợp những công thức tính diện tích hình thoi mà bạn có thể tham khảo:

Công thức tính diện tích hình thoi

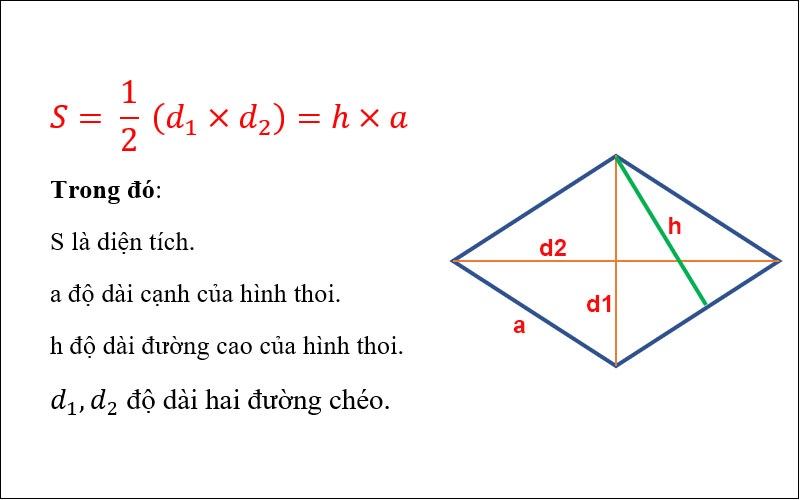
Công thức tính diện tích hình thoi

Công thức tính diện tích hình thoi là S = d1 * d2/2, trong đó d1 và d2 lần lượt là độ dài hai đường chéo của hình thoi.

Để tính diện tích hình thoi, bạn cần biết độ dài của hai đường chéo. Đường chéo chính là đường nối hai đỉnh đối diện của hình thoi, đường chéo phụ là đường nối hai đỉnh còn lại.

Khi bạn có độ dài của hai đường chéo, hãy sử dụng công thức S = d1 * d2 / 2 để tính diện tích. Bạn nhân độ dài đường chéo chính (d1) với độ dài đường chéo phụ (d2) rồi chia kết quả cho nhau.

Giả sử bạn có một hình thoi có đường chéo chính dài 8 cm và đường chéo phụ dài 6 cm. Nếu áp dụng công thức S = d1 * d2 / 2, chúng ta nhận được:

S = 8 cm * 6 cm / 2

= 48 cm² / 2

= 24 cm²

Vậy diện tích của hình thoi trong ví dụ này là 24cm2.

Công thức tính diện tích một hình thoi bằng hệ thức lượng trong tam giác

Để tính diện tích một hình thoi bằng công thức tam giác, bạn có thể sử dụng công thức sau:

Diện tích = (Cạnh x Cạnh x sin(độ) / 2

Trong đó cạnh là độ dài của một cạnh tính bằng độ hình thoi và độ là một góc trong hình thoi (thường là góc giữa hai cạnh chéo).

Ví dụ: Nếu bạn có một hình thoi có độ dài cạnh 5 đơn vị và góc giữa hai cạnh chéo là 60 độ, bạn có thể tính diện tích như sau:

Diện tích = (5 x 5 x sin(60) ) / 2 = (25 x √3) / 2 ≈ 21,65 đơn vị vuông.

Công thức này dựa trên công thức tam giác, trong đó diện tích của một tam giác bằng một nửa tích hai cạnh và sin của góc giữa hai cạnh đó. Vì hình thoi có hai cạnh bằng nhau và góc giữa hai cạnh chéo là 90 độ nên công thức trên là cách tính diện tích một hình thoi bằng công thức tam giác.

Công thức tính diện tích một hình thoi bằng cạnh đáy và chiều cao

Để tính diện tích một hình thoi dựa trên đáy và chiều cao, bạn có thể sử dụng công thức sau:

Diện tích = (Cạnh x Chiều cao) / 2.

Trong đó đáy là chiều dài một cạnh của hình thoi và chiều cao là chiều dài từ cạnh đến đến đỉnh tương ứng với cạnh đó.

Ví dụ: Nếu bạn có một hình thoi có diện tích đáy là 6 đơn vị và chiều cao tương ứng là 4 đơn vị, bạn có thể tính diện tích như sau:

Diện tích = (6 x 4) / 2 = 24/2 = 12 đơn vị vuông.

Cách tính diện tích một hình thoi bằng đường kính

Để tính diện tích một hình thoi dựa trên đường kính của nó, bạn có thể sử dụng công thức sau:

Diện tích = (Đường kính x Đường kính) / 2.

Trong đó đường kính là chiều dài đường kính của hình thoi.

Ví dụ: nếu bạn có hình thoi có đường kính 10 đơn vị, bạn có thể tính diện tích như sau:

Diện tích = (10 x 10) / 2 = 100/2 = 50 đơn vị vuông.

Công thức tính diện tích hình thoi lớp 4

Để tính diện tích hình thoi, học sinh lớp 4 thường sử dụng công thức đơn giản Diện tích = Cạnh x Cạnh / 2.

Giả sử cạnh của hình thoi là a, ta có công thức tính diện tích:

Diện tích = a x a/2

Hoặc nếu biết đường chéo của hình thoi, bậc 4 cũng có thể sử dụng công thức Diện tích = đường chéo chính x đường chéo phụ / 2.

Ví dụ: Nếu giả sử hình thoi có cạnh dài 5 cm thì chúng ta có thể tính diện tích như sau:

Diện tích = 5 cm x 5 cm / 2

= 25 cm 2 / 2

= 12,5 cm 2

Vậy diện tích của hình thoi trong ví dụ này là 12,5 cm

Công thức tính diện tích hình thoi lớp 5

Ở lớp 5, để tính diện tích hình thoi, chúng ta sử dụng công thức Diện tích = cạnh x chiều cao, trong đó cạnh là độ dài một cạnh của hình thoi và chiều cao là đoạn thẳng vuông góc với một đỉnh của hình thoi tới cạnh đối diện.

Nếu cạnh của hình thoi được gọi là a và chiều cao được gọi là h thì công thức tính diện tích là:

Diện tích = a x h

Chiều cao h có thể được tính bằng công thức Pythagore, trong đó h² = đường chéo chính - đường chéo phụ.

Điều này giúp tính toán chiều cao nếu chỉ biết đường chéo chính và nửa cạnh của hình thoi.

Giả sử một hình thoi có cạnh dài 6 cm và đường chéo chính dài 10 cm. Đầu tiên chúng ta tính nửa cạnh bằng cách chia cạnh cho 2: nửa cạnh = 6 cm / 2 = 3 cm.

Tiếp theo, chúng ta tính chiều cao bằng công thức Pythagore: h2 = (10 cm) 2 – (3 cm) 2 = 100 cm 2 – 9 cm 2 = 91 cm . Nếu lấy căn bậc hai của 91 thì ta được h ≈ 9,54 cm. Cuối cùng, chúng ta áp dụng công thức tính diện tích: Diện tích ≈ 6 cm x 9,54 cm ≈ 57.24cm2.

Diện tích của hình thoi trong ví dụ này là khoảng 57,24 cm² (làm tròn) với chiều dài cạnh là 6 cm và đường chéo chính là 10 cm.

Cách tìm đường chéo của hình thoi

Để tìm độ dài đường chéo của hình thoi, chúng ta có một số phương pháp phổ biến. Tùy thuộc vào thông tin được cung cấp, bạn có thể sử dụng một trong các phương pháp sau:

Sử dụng công thức Pythagore

Nếu đã biết độ dài hai cạnh liên tiếp của hình thoi, bạn có thể sử dụng công thức Pythagore để tìm độ dài của tính đường chéo. Đường chéo của hình thoi là đường chéo chính và công thức Pythagore phát biểu rằng bình phương của đường chéo chính bằng tổng bình phương của hai cạnh kề. Ví dụ: nếu độ dài hai cạnh kề nhau là a và b thì công thức là: Đường chéo chính 2 = a2 + b2.Sau đó, bạn có thể lấy căn bậc hai của kết quả để tìm độ dài của đường chéo chính.

Sử dụng tính đối xứng và tỷ lệ

Nếu biết độ dài hai cạnh không kề nhau của hình thoi thì có thể sử dụng tính chất đối xứng và tỷ lệ của hình thoi. Vẽ một đường thẳng từ một đỉnh của hình thoi đến trung điểm của cạnh đối diện. Đường này biểu thị chiều cao và cắt đường chéo chính thành hai phần bằng nhau.Từ đó, bạn có thể tính độ dài đường chéo chính bằng cách nhân độ dài cạnh không liền kề với 2.

Cách tìm chiều cao H để tính diện tích hình thoi

Để tính diện tích hình thoi, bạn cần biết cạnh của hình thoi và độ cao (chiều cao) của nó. Cách tìm chiều cao H của hình thoi:

Cách 1: Sử dụng công thức Pythagore

• Biết hai cạnh của hình thoi: a là một cạnh và b là cạnh kia.
• Áp dụng công thức Pytago: H2 = a2 - (b/2)2
• Trong đó b/2 là một nửa cạnh của hình thoi.
• Tính căn bậc hai của H2 để tìm chiều cao của H.

Cách 2: Sử dụng tỉ lệ và tính chất của hình thoi

• Biết hai cạnh không kề nhau của hình thoi: a là một cạnh và b là cạnh kia.
• Vẽ chiều cao từ một đỉnh của hình thoi tới cạnh đối diện. Chiều cao này chia đường chéo chính thành hai phần bằng nhau.
• Sử dụng tỉ số hình thoi: (b/2) / H = a / (2H)
• Trong đó b/2 là một nửa cạnh của hình thoi và H là chiều cao cần xác định.
• Giải phương trình trên để tính chiều cao H.

Ví dụ:

Giả sử bạn có một hình thoi có một cạnh a = 8 cm và cạnh kia b = 6 cm. Để tính chiều cao H, bạn có thể sử dụng cách 1 như sau:

H2 = a2 - (b/2)

H 2 = 8 2 - (6/2) 9

H 2 = 64 - 9

H 2 = 55

H ≈ √ 55 ≈ 7,42 cm

Chiều cao của hình thoi trong ví dụ này là khoảng 7,42 cm (làm tròn).

Cách chứng minh diện tích hình thoi

Để kiểm tra công thức tính diện tích của hình thoi, chúng ta có thể sử dụng các phương pháp khác nhau. Đây là một cách để chứng minh điều này bằng cách sử dụng các phép biến đổi hình học:

Giả sử một hình thoi có cạnh a và chiều cao h tính từ đỉnh này sang cạnh đối diện.

• Bước 1: Vẽ hình thoi và một đường chéo chính đi qua hai góc của hình thoi.
• Bước 2: Chia hình thoi thành hai hình tam giác theo đường chéo chính. Điều này tạo ra hai hình tam giác giống nhau vì chúng có cùng góc và cạnh giống nhau
• Bước 3: Gọi tên cạnh hình thoi a và chiều cao h. Chúng ta có thể chứng minh rằng mọi tam giác đều có diện tích 0,5 * a * h.
• Bước 4: Tổng diện tích của hai tam giác đồng dạng là S = 2 * (0,5 * a * h) = a * h.
• Bước 5: Vì hai tam giác đồng dạng tạo thành hình thoi nên tổng diện tích của hai tam giác này cũng bằng diện tích của hình thoi ban đầu.

Từ đó ta kết luận diện tích hình thoi là S = a * h.

Đây là một cách chứng minh đơn giản về công thức tính diện tích của hình thoi bằng cách sử dụng các hình tam giác và các phép biến đổi hình học.

Cách vẽ một hình thoi chính xác nhất

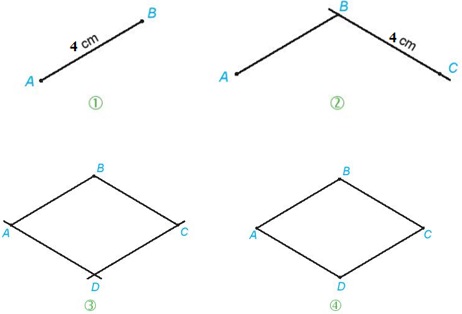
Cách vẽ một hình thoi chính xác nhất

Để vẽ một hình thoi chính xác, bạn có thể làm theo các bước sau:

• Bước 1: Chuẩn bị các dụng cụ vẽ như bút mực, bút chì, thước kẻ và compa.
• Bước 2: Đặt điểm gốc để xác định vị trí của hình thoi trên giấy.
• Bước 3: Dùng thước vẽ hai đường thẳng nằm ngang, song song. Độ dài của hai đường thẳng này tương ứng với hai cạnh của hình thoi.
• Bước 4: Xác định trung điểm của hai đường thẳng nằm ngang.Dùng compa vẽ một cung cong từ điểm này để cắt hai đường thẳng song song. Giao điểm này sẽ là một đỉnh của hình thoi.
• Bước 5: Tiếp tục vẽ các cung cong từ các đỉnh còn lại để tạo thành hình thoi. Đảm bảo các cạnh và góc của hình thoi đều và chính xác.
• Bước 6: Dùng thước kẻ và bút chì để hình thoi được rõ nét và chính xác hơn.Xóa các hướng dẫn không cần thiết và chỉ giữ lại toàn bộ hình thoi

Bài tập áp dụng

Bài tập 1:

Hình thoi ABCD có cạnh a = 6 cm và đường cao h = 8 cm. Tính diện tích của hình thoi này.

Đáp án:

Diện tích = a * h = 6 cm * 8 cm = 48 cm².

Bài tập 2:

Hình thoi ABCD có cạnh a = 10 m và đường chéo d = 12 m. Tính diện tích của hình thoi này.

Đáp án:

Đường cao của hình thoi có thể tính bằng công thức Pythagoras:

H² = (d/2)² - (a/2)²

H² = (12 m / 2)² - (10 m / 2)²

H² = 36 m² - 25 m²

H² = 11 m²

H ≈ √11 ≈ 3.32 m

Diện tích = a * H = 10 m * 3.32 m = 33.2 m².

Bài tập 3:

Hình thoi ABCD có cạnh a = 7 cm và góc α = 60°. Tính diện tích của hình thoi này.

Đáp án:

Đường cao của hình thoi có thể tính bằng cách sử dụng công thức sin:

H = a * sin(α)

H ≈ 7 cm * sin(60°)

H ≈ 7 cm * 0.866 (là giá trị xấp xỉ của sin(60°))

H ≈ 6.062 cm

Diện tích = a * H = 7 cm * 6.062 cm = 42.434 cm².

Bài tập 4:

Hình thoi ABCD có cạnh a = 12 m và đường cao h = 9 m. Tính diện tích của hình thoi này.

Đáp án:

Diện tích = a * h = 12 m * 9 m = 108 m².

Bài tập 5:

Hình thoi ABCD có cạnh a = 5 cm và cạnh khác b = 8 cm. Tính diện tích của hình thoi này.

Đáp án:

Đường cao của hình thoi có thể tính bằng công thức Pythagoras:

H² = a² - (b/2)²

H² = 5 cm² - (8 cm / 2)²

H² = 5 cm² - 4 cm²

H² = 1 cm²

H ≈ √1 = 1 cm

Diện tích = a * H = 5 cm * 1 cm = 5 cm².

Bài tập 6:

Hình thoi ABCD có cạnh a = 15 m và góc α = 45°. Tính diện tích của hình thoi này.

Đáp án:

Đường cao của hình thoi có thể tính bằng cách sử dụng công thức cos:

H = a * cos(α)

H ≈ 15 m * cos(45°)

H ≈ 15 m * 0.707 (là giá trị xấp xỉ của cos(45°))

H ≈ 10.605 m

Diện tích = a * H = 15 m * 10.605 m = 159.075 m².

Trên đây là những thông tin thayphu.net đã giải thích về diện tích hình thoi khi giải bài tập tính diện tích của hình thoi, chúng ta đã học được cách tính diện tích dựa vào các yếu tố như cạnh, chiều cao và các góc của hình thoi. Kiến thức này có thể áp dụng trong nhiều tình huống thực tế và đóng vai trò quan trọng trong các nguyên tắc cơ bản của hình học và toán học.