Diện tích hình thang, định nghĩa và các phương pháp tính

Cách tính diện tích hình thang phụ thuộc vào loại hình và thông tin có sẵn về các đoạn thẳng trong hình, dưới đây là tổng hợp công thức và cách tính.

Hình thang là một hình học đơn giản nhưng thú vị và việc tính diện tích của nó là một trong những khái niệm cơ bản của hình học. Nếu hiểu rõ công thức và cách tính, bạn có thể dễ dàng áp dụng để tính diện tích của bất kỳ hình thang nào. Hãy cùng thayphu tìm hiểu chi tiết cách tính diện tích hình thang và áp dụng vào các ví dụ cụ thể.

Định nghĩa và đặc điểm hình thang

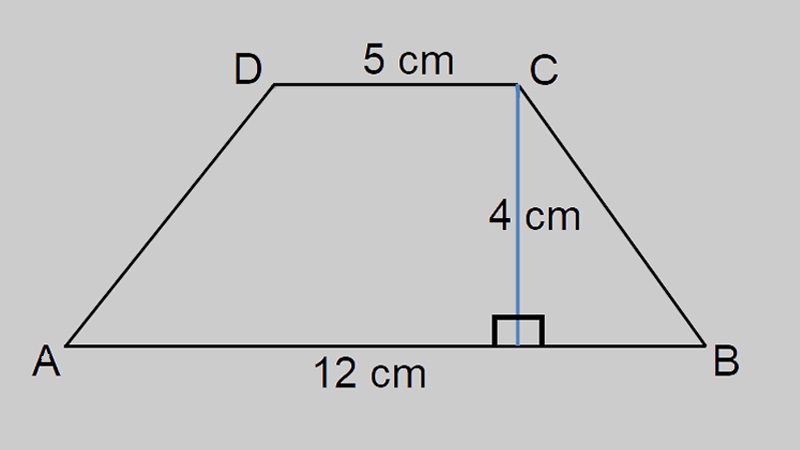
Định nghĩa và đặc điểm của công thức tính diện tích hình thang

Hình thang là một hình hình học có bốn cạnh trong đó hai cạnh đối diện song song và có độ dài khác nhau. Chiều cao của hình thang là đoạn thẳng nối hai đỉnh không song song với nhau.

Các tính chất đặc biệt của hình thang

Hình thang có những tính chất đặc biệt sau:

• Hai cạnh đối diện của hình thang song song: Nghĩa là hai cạnh không song song của hình thang luôn cùng hướng và không cắt nhau.
• Chiều cao của hình thang: Chiều cao của hình thang là đoạn thẳng nối hai đỉnh không song song với nhau và vuông góc với hai cạnh song song. Chiều cao chia hình thang thành hai tam giác cân, các đỉnh của tam giác có các cạnh song song.
• Trung điểm của hai cạnh không song song: Trung điểm của hai cạnh không song song của hình thang là điểm có cùng độ cao và cách hai đỉnh không song song một khoảng như nhau.
• Tổng độ dài hai đáy của hình thang bằng tổng độ dài hai cạnh không song song: Nghĩa là tổng độ dài hai cạnh không song song của hình thang bằng nhau bằng tổng độ dài hai đáy của nó.
• Diện tích hình thang bằng tổng diện tích của hai tam giác cân: Diện tích hình thang bằng tổng diện tích của hai tam giác cân tạo bởi hai cạnh không song song và chiều cao.

Phân loại các hình thang mà bạn không nên bỏ qua

Khi phân loại hình thang, có một số loại bạn không nên bỏ qua.

Hình thang cân

Đây là loại hình thang có hai cạnh đáy bằng nhau và hai cạnh bằng nhau. Góc giữa hai cạnh dưới cũng giống nhau. Đối xứng qua trục đối xứng dọc theo chiều cao đi qua đỉnh hình thang.

Hình thang đều

Góc giữa hai cạnh dưới cũng giống nhau. Đối xứng qua trục đối xứng dọc theo chiều cao đi qua đỉnh hình thang.

Hình thang vuông

Một cặp cạnh bên gồm có chiều cao và đáy vuông góc với nhau.

Hình thang tổng quát

Có thể có các cạnh dưới và cạnh có độ dài khác nhau, các góc không bằng nhau và thiếu tính đối xứng.

Công thức tính diện tích hình thang mà bạn nên biết

Công thức tính diện tích hình thang là:

Diện tích = 1/2 x (chiều dài cạnh thứ nhất + chiều dài cạnh thứ hai) x chiều cao Trong đó:

Chiều dài cạnh thứ nhất và cạnh thứ hai là hai cạnh không song song của hình thang.

Độ cao là đoạn thẳng vuông góc với hai cạnh song song và đi qua giao điểm của hai cạnh đó.

Công thức trên dựa trên nguyên tắc diện tích hình thang bằng nửa tổng chiều dài hai đáy nhân với chiều cao. Để áp dụng công thức này chúng ta cần biết độ dài hai cạnh không song song và độ dài chiều cao của hình thang.

Cách tính diện tích hình thang khi biết các cạnh yêu cầu tìm h

Để tính diện tích hình thang nếu biết các cạnh cần thiết, bạn có thể làm theo các bước sau:

• Bước 1:Tìm độ dài hai cạnh không song song của hình thang. Gọi chúng là a và b.
• Bước 2:Xác định kinh độ và chiều cao của hình thang.Độ cao là đoạn thẳng vuông góc với hai cạnh song song và đi qua giao điểm của hai cạnh đó. Gọi kinh độ là độ cao h.
• Bước 3:Áp dụng công thức tính diện tích hình thang: Diện tích = 1/2 x (a + b) x h.
• Bước 4:Thực hiện các phép tính theo công thức tính diện tích hình thang.

Sau khi hoàn thành các bước trên, bạn sẽ có được diện tích hình thang dựa trên các cạnh đã biết.

Cách tính diện tích hình thang khi biết h và một cạnh

Để tính diện tích hình thang có chiều cao (h) và một cạnh (a hoặc b), bạn có thể sử dụng công thức sau:

Diện tích = (cạnh đáy lớn + cạnh đáy nhỏ) x chiều cao / 2 Trong công thức này, diện tích có thể được tính bằng cách chỉ cần biết một cạnh của đáy (cạnh đáy lớn hoặc cạnh đáy nhỏ) và chiều cao của hình thang.

Ví dụ: Nếu bạn biết chiều cao (h) và đáy lớn nhất (a), công thức tính diện tích là: Diện tích = (a + b) x h / 2 Nếu bạn biết chiều cao (h) và cạnh nhỏ (b).

Công thức tính diện tích là: . diện tích = (a + b) x h / 2...

Cách tính diện tích thang từ thể tích

Để tính diện tích hình thang từ thể tích của nó, bạn cần biết thể tích và chiều cao của hình thang.

Công thức tính diện tích hình thang theo thể tích là:

Diện tích = Thể tích / Chiều cao

Điều này có nghĩa là bạn chia thể tích hình thang cho chiều cao của nó để tính diện tích. Ví dụ: Giả sử bạn có một hình thang có thể tích 1000 cm³ và chiều cao 20 cm. Để tính diện tích hình thang, hãy sử dụng công thức:

Diện tích = 1000 cm³ / 20 cm = 50 cm²

Vậy diện tích hình thang trong trường hợp này là 50 cm².

Chứng minh công thức diện tích hình thang đặc biệt

Để chứng minh công thức tính diện tích hình thang, chúng ta có thể sử dụng phương pháp tam giác.

Giả sử chúng ta có một hình thang có hai cạnh không song song có chiều dài a và b và chiều cao h.Để chứng minh công thức tính diện tích, ta chia hình thang thành hai hình tam giác.

Tam giác thứ nhất: Đây là một tam giác có cạnh a và chiều cao là h.

Diện tích của tam giác thứ nhất là: S1 = 1/2 x a x h. Tam giác thứ hai: Đây là tam giác có đáy là cạnh b và chiều cao là h.

Diện tích của tam giác thứ hai là: S2 = 1/2 x w x h. Tổng diện tích của hai tam giác này là:

S = S1 + S2 = 1/2 x a x h + 1/2 x b x h.

Rút gọn biểu thức ta được:

S = (1/2)(a + b)h.

Bây giờ chúng ta đã chứng minh được công thức tính diện tích hình thang: Diện tích = 1/2 x (a + b) x h.

Chia hình thang thành hai hình tam giác và tính diện tích mỗi tam giác giúp chúng ta hiểu rõ hơn nguyên lý cơ bản của công thức tính diện tích hình thang.

Những phương pháp giải bài toán diện tích hình thang

Để giải bài toán tính diện tích hình thang, bạn có thể sử dụng một số phương pháp hiệu quả.

Dưới đây là một số cách tính phổ biến:

Sử dụng công thức tính diện tích hình thang

Công thức tính diện tích hình thang là Diện tích = 1/2 x (a + b) x h, trong đó a và b là độ dài hai cạnh không song song và h là kinh độ của độ cao. Nếu bạn đã biết đủ thông tin về các cạnh và chiều cao của hình thang, bạn chỉ cần nhập các giá trị vào công thức để tính diện tích.

Tính chất sử dụng của hình thang

Hình thang có một số tính chất đặc biệt như chiều cao chia hình thang thành hai tam giác cân, tổng độ dài hai đáy bằng tổng độ dài hai cạnh không song song. Các thuộc tính này cho phép bạn phân tích hình thang thành các dạng hình học đơn giản hơn như hình tam giác và hình chữ nhật để tính diện tích.

Sử dụng tính đối xứng

Trong một số trường hợp, bạn có thể sử dụng tính đối xứng để tạo một hình thang có diện tích đã biết.

Ví dụ: Nếu bạn đã biết diện tích của một hình thang và các cạnh của nó, bạn có thể sử dụng tính đối xứng để tạo một hình thang khác có diện tích tương tự nhưng các cạnh khác nhau.Sau đó, bạn có thể tính diện tích hình thang mới bằng các phương pháp khác.

Sử dụng các phương pháp hình học khác

Ngoài phương pháp trực tiếp là sử dụng công thức, các em cũng có thể sử dụng các phương pháp hình học khác để giải bài toán.

Ví dụ: Nếu bạn tìm thấy một hình vuông hoặc hình chữ nhật có cùng diện tích với hình thang, bạn có thể sử dụng diện tích của hình vuông hoặc hình chữ nhật để tính diện tích hình thang.

Lưu ý khi giải một bài toán về diện tích hình thang

Khi giải bài toán về diện tích hình thang, bạn cần lưu ý một số điều quan trọng như sau:

• Xác định thông tin đã biết: Đầu tiên, hãy đọc và hiểu kỹ bài toán để xác định thông tin đã biết về hình thang. Điều này bao gồm độ dài cạnh, đáy, chiều cao hoặc thông tin khác về hình thang.
• Vẽ hình thang: Vẽ hình thang lên một tờ giấy để thể hiện rõ hình và các thông tin đã biết.Điều này giúp bạn dễ dàng hình dung và làm việc với các hình thang hơn.
• Sử dụng công thức tính diện tích hình thang: Nếu đã biết đủ thông tin về cạnh và chiều cao của hình thang thì bạn hãy áp dụng công thức tính diện tích hình thang (diện tích = 1/2 x (a + b) x h) để tính diện tích.
• Áp dụng tính chất của hình thang: Nếu chưa có đủ thông tin để sử dụng công thức tính diện tích, hãy xét tính chất của hình thang.Ví dụ, chiều cao chia hình thang thành hai tam giác cân có diện tích bằng nhau.
• Chú ý đơn vị đo: Khi tính diện tích hình thang phải sử dụng cùng đơn vị đo cạnh và chiều cao để đảm bảo kết quả chính xác.
• Kiểm tra kết quả: Sau khi tính diện tích hình thang, bạn kiểm tra lại kết quả của mình. Đảm bảo rằng các phép tính đã được thực hiện chính xác và kết quả là hợp lý dựa trên thông tin đã biết.Những thủ thuật trên sẽ giúp bạn giải quyết các vấn đề về mặt hình thang một cách chính xác và hiệu quả.

Bài tập áp dụng

Bài tập 1:

Hình thang ABCD có đáy lớn AB và đáy nhỏ CD. Đường cao h của hình thang này là 8 cm. Đáy lớn AB có độ dài 15 cm và đáy nhỏ CD có độ dài 9 cm. Tính diện tích của hình thang ABCD.

Đáp án:

Để tính diện tích hình thang, ta áp dụng công thức: Diện tích = 1/2 x (đáy lớn + đáy nhỏ) x đường cao.

Diện tích hình thang ABCD = 1/2 x (15 cm + 9 cm) x 8 cm = 96 cm².

Bài tập 2:

Hình thang MNPQ có đáy lớn MN và đáy nhỏ PQ. Đường cao h của hình thang này là 12 cm. Đáy lớn MN có độ dài 20 cm và diện tích của hình thang là 240 cm². Tính độ dài của đáy nhỏ PQ.

Đáp án:

Để tính độ dài của đáy nhỏ PQ, ta sử dụng công thức diện tích hình thang: Diện tích = 1/2 x (đáy lớn + đáy nhỏ) x đường cao.

240 cm² = 1/2 x (20 cm + đáy nhỏ) x 12 cm

480 = (20 cm + đáy nhỏ) x 12 cm

40 + đáy nhỏ = 40 cm

đáy nhỏ = 40 cm - 20 cm

đáy nhỏ = 20 cm.

Bài tập 3:

Hình thang ABCD có đáy lớn AB và đáy nhỏ CD. Đường cao h của hình thang này là 10 cm. Diện tích của hình thang là 80 cm² và đáy lớn AB có độ dài 16 cm. Tính độ dài của đáy nhỏ CD.

Đáp án:

Áp dụng công thức diện tích hình thang: Diện tích = 1/2 x (đáy lớn + đáy nhỏ) x đường cao.

80 cm² = 1/2 x (16 cm + đáy nhỏ) x 10 cm

160 = (16 cm + đáy nhỏ) x 10 cm

16 cm + đáy nhỏ = 16 cm

đáy nhỏ = 16 cm - 16 cm

đáy nhỏ = 0 cm.

Bài tập 4:

Hình thang ABCD có đáy lớn AB và đáy nhỏ CD. Đường cao h của hình thang này là 6 cm. Diện tích của hình thang là 45 cm² và đáy nhỏ CD có độ dài 9 cm. Tính độ dài của đáy lớn AB.

Đáp án:

Áp dụng công thức diện tích hình thang: Diện tích = 1/2 x (đáy lớn + đáy nhỏ) x đường cao.

45 cm² = 1/2 x (đáy lớn + 9 cm) x 6 cm

90 = (đáy lớn + 9 cm) x 6 cm

đáy lớn + 9 cm = 15 cm

đáy lớn = 15 cm - 9 cm

đáy lớn = 6 cm.

Bài tập 5:

Hình thang ABCD có đáy lớn AB và đáy nhỏ CD. Đường cao h của hình thang này là 12cm. Đáy lớn AB có độ dài 18cm và đáy nhỏ CD có độ dài 8 cm. Tính diện tích của hình thang ABCD.

Đáp án:

Để tính diện tích hình thang, ta áp dụng công thức: Diện tích = 1/2 x (đáy lớn + đáy nhỏ) x đường cao.

Diện tích hình thang ABCD = 1/2 x (18 cm + 8 cm) x 12 cm = 156 cm².

Kết luận

Kết thúc, việc giải quyết các bài toán về diện tích hình thang đòi hỏi sự hiểu biết về các công thức và tính chất của hình thang, cùng với khả năng áp dụng chúng vào thực tế. Việc tìm hiểu và làm quen với các bài tập tự luận giúp bạn rèn luyện kỹ năng tư duy logic và tính toán.