Tính diện tích hình bình hành, tổng hợp công thức và bài tập

Cách tính diện tích hình bình hành dùng để tìm các góc các cạnh giữa các hình với nhau.Định nghĩa ,tính chất cách áp dụng.

Trong toán học và hình học, hình bình hành là một hình hình học có những tính chất độc đáo và thú vị. Một trong những khía cạnh quan trọng của hình bình hành là tính diện tích của nó, tức là diện tích bên trong hình.Trong bài viết này, chúng ta sẽ khám phá các phương pháp khác nhau về cách tính diện tích hình bình hành. Bằng cách áp dụng các công thức và quy tắc hình học đơn giản, chúng ta có thể dễ dàng cách tính diện tích hình bình hành từ các tham số như cạnh, chiều cao và góc giữa các cạnh. Cùng thayphu xem ngay nhé.

Định nghĩa hình bình hành trong hình học

Hình bình hành được định nghĩa như thế nào trong hình học

Hình bình hành là đa giác có bốn cạnh. Các cạnh song song và có cùng độ dài. Đồng thời, các cạnh chéo của hình bình hành cắt nhau ở tâm.

Hình bình hành có nhiều cách gọi, bao gồm hình vuông, hình chữ nhật và hình bình hành nói chung. Đặc biệt, hình vuông là một dạng hình bình hành đặc biệt trong đó bốn cạnh và bốn góc đều có cùng chiều dài.

Hình bình hành được chia làm bao nhiêu loại

Hình bình hành có thể được phân thành nhiều loại khác nhau dựa trên tính chất và đặc điểm của chúng. Một số loại hình bình hành thông dụng được liệt kê dưới đây: Hình bình hành tổng quát: Đây là dạng hình bình hành tổng quát nhất. Có bốn cạnh song song và các cạnh đối diện có độ dài bằng nhau. Góc giữa hai cạnh kề nhau có thể có giá trị bất kỳ.

• Hình vuông: Đây là một loại hình bình hành đặc biệt. Có bốn cạnh bằng nhau và bốn góc đều bằng 90 độ. Các đường chéo của hình vuông cắt nhau theo chiều dọc ở tâm.
• Hình chữ nhật :Đây cũng là một loại hình bình hành đặc biệt. Có bốn cạnh song song và bốn góc, tất cả đều bằng 90 độ. Đặc biệt, các đường chéo của hình chữ nhật giao nhau ở giữa.

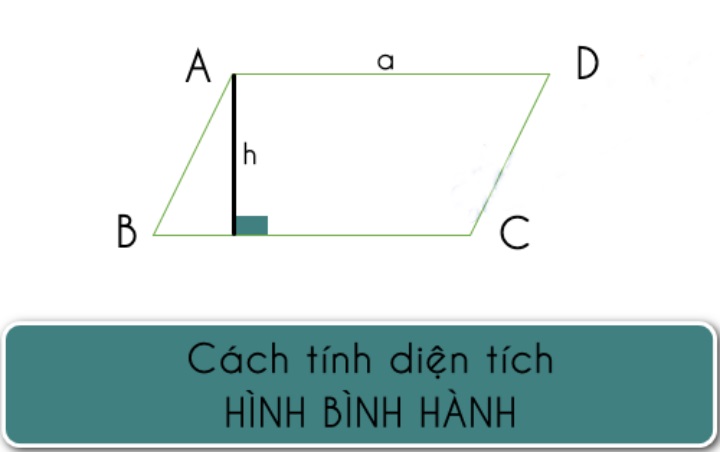
Công thức tính diện tích hình bình hành trong hình học

Cách tính tính diện tích hình bình hành phụ thuộc vào thông tin cụ thể về hình học của nó. Dưới đây là các công thức tính diện tích hình bình hành thông dụng:

Tính diện tích theo cạnh và chiều cao

Đo độ dài một cạnh của hình bình hành (a).

Đo độ dài đoạn thẳng từ đỉnh tương ứng với cạnh được chọn đến đường thẳng song song với cạnh đó (h).

Diện tích (A) của hình bình hành được tính bằng công thức A = a * h.

Tính diện tích theo đường chéo

Đo độ dài đường chéo dài (d1) và đường chéo ngắn (d2) của hình bình hành. Diện tích (A) của hình bình hành được tính bằng công thức A = (d1 * d2) / 2.

Lưu ý công thức tính diện tích này chỉ áp dụng cho hình bình hành tổng quát. Đối với các loại hình bình hành đặc biệt, chẳng hạn như hình vuông và hình chữ nhật, có các công thức tính diện tích tương ứng.

Ví dụ, đối với một hình vuông, diện tích (A) có thể được tính bằng công thức A = a^2, trong đó a là độ dài cạnh. Đối với hình chữ nhật, diện tích (A) có thể được tính bằng công thức A = a * b, trong đó a và b là độ dài của hai cạnh kề nhau.

Cách tìm chiều cao hình bình hành chi tiết

Để tìm chiều cao của hình bình hành, có nhiều phương pháp khác nhau tùy thuộc vào thông tin có sẵn. Dưới đây là các phương pháp phổ biến để tìm chiều cao của hình bình hành:

Tính chiều cao từ cạnh và diện tích

Nếu biết độ dài một cạnh của hình bình hành (a) và diện tích của nó (A) , bạn có thể tính chiều cao (h) bằng công thức: h = A/a.

Tính chiều cao từ đường chéo

Nếu biết độ dài đường chéo dài (d1) và đường chéo ngắn (d2) của hình bình hành, bạn có thể tính chiều cao (h) bằng công thức: h = ( 2*A)/d1, trong đó A là diện tích hình bình hành.

Tính chiều cao từ góc giữa hai cạnh

Nếu đã biết độ lớn góc giữa hai cạnh kề nhau trong hình bình hành thì có thể tính chiều cao bằng công thức lượng giác. Phương pháp này có thể yêu cầu kiến thức về sin, cosin hoặc tan của góc.

Các phương pháp tính diện tích hình bình hành

Để giải một bài toán liên quan đến hình bình hành, có thể sử dụng nhiều phương pháp và kỹ thuật khác nhau. Dưới đây là một số phương pháp giải hình học thông dụng có liên quan đến hình bình hành:

Sử dụng công thức tính diện tích

Đối với các bài toán yêu cầu tính diện tích hình bình hành, các em có thể sử dụng công thức tính diện tích thích hợp để tính diện tích hình bình hành.

Ví dụ: Nếu biết chiều dài một cạnh và chiều cao, em có thể sử dụng công thức tính diện tích A = a * h để tính diện tích.

Sử dụng quy tắc đối xứng và bằng nhau

Hình bình hành có nhiều đặc điểm đối xứng như các cạnh song song và các góc đối bằng nhau.

Sử dụng các quy tắc đối xứng và đẳng thức trong hình học, bạn có thể tìm thấy các giá trị và mối quan hệ giữa các cạnh, góc và đường chéo của hình bình hành.

Vận dụng Định lý Pythagore

Định lý Pythagore là một công cụ quan trọng trong hình học và có thể ứng dụng để giải các bài toán liên quan đến hình bình hành.

Ví dụ: Bạn có thể sử dụng định lý Pythagore để tính độ dài đường chéo dựa trên thông tin về các cạnh của hình bình hành.

Cách sử dụng các quy tắc lượng giác

Lượng giác là một công cụ đắc lực để giải các bài toán hình học, trong đó có các bài toán liên quan đến hình bình hành.

Sử dụng các quy tắc sin, cos và tan, bạn có thể tính các giá trị góc, đường chéo hoặc chiều cao của hình bình hành.

Ứng dụng của hình bình hành trong toán học

Hình bình hành có nhiều ứng dụng trong toán học. Dưới đây là một số ví dụ về cách sử dụng phổ biến của hình bình hành:

Diện tích và chu vi

Hình bình hành được dùng để tính diện tích và chu vi trong nhiều bài toán hình học. Các công thức tính diện tích và chu vi hình bình hành là các công thức toán học cơ bản.

Hình học Vecto

Hình bình hành được sử dụng trong hình học vectơ để biểu diễn vectơ. Hai cạnh của hình bình hành biểu diễn hai vectơ, điều này cho phép chúng ta thực hiện các phép tính vectơ như cộng, trừ và nhân với đại số vô hướng.

Hình học ứng dụng

Hình bình hành có thể được sử dụng để mô hình hóa và giải các bài toán hình học ứng dụng. Trong hình học không gian, hình bình hành có thể được sử dụng, chẳng hạn, để mô hình các hình khối và các hình khối tương tự khác.

Bài tập áp dụng

Bài tập 1:

Cho một hình bình hành ABCD với độ dài cạnh AB là 6cm và độ dài đường chéo AC là 10 cm. Tính diện tích của hình bình hành này.

Đáp án:

Để tính diện tích hình bình hành, chúng ta có công thức A = AB * h, trong đó AB là độ dài một cạnh và h là chiều cao. Vì đường chéo AC cắt nhau thành hai tam giác vuông cân, nên chiều cao h bằng một nửa độ dài đường chéo AC. Do đó, h = 10 cm / 2 = 5 cm. Từ đó, diện tích A = 6 cm * 5 cm = 30 cm^2.

Bài tập 2:

Cho một hình bình hành ABCD với độ dài cạnh AB là 8 cm và độ dài một đường chéo AD là 12 cm. Tính chu vi của hình bình hành này.

Đáp án:

Chu vi của hình bình hành có thể được tính bằng cách nhân độ dài cạnh AB với 4, vì cạnh AB và cạnh AD của hình bình hành có cùng độ dài. Vì vậy, chu vi = AB * 4 = 8 cm * 4 = 32 cm.

Bài tập 3:

Cho một hình bình hành ABCD với độ dài cạnh AB là 5 cm và độ dài đường chéo AC là 6 cm. Tính độ dài cạnh AD của hình bình hành.

Đáp án:

Trong hình bình hành, cạnh AB và cạnh AD có cùng độ dài. Vì vậy, độ dài cạnh AD là 5 cm.

Bài tập 4:

Cho một hình bình hành ABCD với độ dài cạnh AB là 7 cm và góc giữa hai cạnh kề nhau là 60 độ. Tính diện tích của hình bình hành này.

Đáp án:

Để tính diện tích hình bình hành, chúng ta có thể sử dụng công thức A = AB * h, trong đó AB là độ dài một cạnh và h là chiều cao. Với góc giữa hai cạnh kề nhau là 60 độ, chúng ta có thể sử dụng công thức h = AB * sin(60 độ) để tính chiều cao. Vì sin(60 độ) = √3 / 2, nên h = 7 cm * (√3 / 2) = (7√3) / 2 cm. Từ đó, diện tích A = 7 cm * (7√3) / 2 cm = (49√3) / 2 cm^2.

Bài tập 5:

Cho một hình bình hành ABCD với độ dài cạnh AB là 10 cm và độ dài đường chéo AD là 8 cm. Tính độ dài đường chéo BC của hình bình hành.

Đáp án:

Trong hình bình hành, đường chéo AD và đường chéo BC có cùng độ dài. Vì vậy, độ dài đường chéo BC là 8 cm.

Kết luận

Trên đây là một số ứng dụng và ví dụ về hình bình hành trong toán học. Hình bình hành không chỉ có giá trị trong lĩnh vực hình học, mà còn được áp dụng rộng rãi trong các lĩnh vực khác như đại số tuyến tính, hình học vector và mật mã học.