Cách xác định đa thức một biến và bài tập vận dụng

Đa thức một biến là một biểu thức toán học được tạo thành từ một biến duy nhất và các hệ số số học. Biến này thường được ký hiệu là x.

Đa thức của một biến là một khái niệm cơ bản trong toán học và được sử dụng rộng rãi trong nhiều lĩnh vực như đại số, giải tích và giải tích. Đa thức một biến được coi là một công cụ giúp chúng ta lập mô hình và giải quyết nhiều vấn đề phức tạp trong thế giới thực.

Trong bài viết này, chúng ta sẽ cùng thayphu xem xét cách xây dựng, biểu diễn và thực hiện các phép toán đa thức một biến.

Khái niệm đa thức của một biến

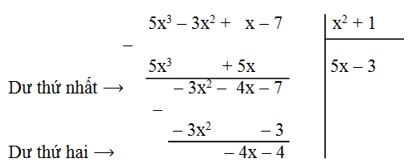
Khái niệm về đa thức một biến

Đa thức một biến có thể có bậc khác nhau tùy thuộc vào lũy thừa cao nhất của biến trong đa thức. Ví dụ: đa thức bậc nhất có dạng ax + b, trong đó a và b là các hệ số và đa thức bậc hai có dạng ax^2 + bx + c.

Một đa thức có thể có nhiều hơn hai số hạn và các số hạng này có thể có bậc khác nhau. Một đặc điểm quan trọng của chúng là khả năng thực hiện các phép toán cơ bản như cộng, trừ, nhân và chia.

Khi thực hiện các thao tác này, chúng ta kết hợp các số hạng tương ứng theo các quy tắc toán học.Nó cho chúng ta cơ hội biểu diễn các mối quan hệ toán học phức tạp. Với đa thức, chúng ta có thể mô hình hóa các quy luật tự nhiên, các mối quan hệ kinh tế, các phương trình vật lý và hơn thế nữa. Điều này giúp chúng ta phân tích và giải được nhiều bài toán thực tế bằng phương pháp toán học. Nó cũng có thể được sử dụng để dự đoán xu hướng và mô phỏng các hiện tượng. Bằng cách thu thập dữ liệu thực và tìm mô hình đa thức phù hợp, chúng ta có thể xác định xu hướng, dự đoán giá trị trong tương lai và hiểu được sự phụ thuộc giữa các biến khác nhau.

Các dạng thường gặp một đa thức của một biến

Có một số dạng đa thức phổ biến trong đa thức một biến, bao gồm:

Đa thức đơn giản

Đa thức đơn giản là đa thức chứa một số hạng duy nhất. Ví dụ: f(x) = 3x^2 - 5x + 2 là một đa thức đơn giản.

Đa thức đầy đủ

Đa thức đầy đủ là đa thức có tất cả các bậc từ 0 đến bậc cao nhất.Ví dụ: f(x) = 2x^3 - x^2 + 4x - 7 là đa thức đầy đủ bậc 3.

Đa thức thuần nhất

Đa thức thuần nhất là đa thức trong đó tất cả các số hạng đều có cùng hạng. Ví dụ: f(x) = 4x^2 + 2x^2 - 3x^2 là một đa thức thuần nhất.

Đa thức khối

Đa thức khối là loại đa thức có hệ số là các đa thức khác. Ví dụ: f(x) = (x^2 + 1)(x^3 - 2x + 3) là đa thức bậc ba.

Hướng dẫn cách xác định một đa thức của một biến mới nhất

Để xác định một đa thức một biến, chúng ta cần làm các bước sau đây:

Bước 1: Xác định các hạng tử

Quan sát biểu thức và xác định các hạng tử có trong đa thức. Mỗi hạng tử bao gồm một hệ số và một mũ của biến.

Ví dụ: Trong đa thức f(x) = 3x^2 - 5x + 2, chúng ta có ba hạng tử: 3x^2, -5x, và 2.

Bước 2: Xác định bậc của đa thức

Bậc của đa thức là mũ cao nhất của biến trong đa thức.

Để xác định bậc, chúng ta kiểm tra mũ của tất cả các hạng tử và chọn mũ cao nhất.

Ví dụ: Trong đa thức f(x) = 3x^2 - 5x + 2, bậc của đa thức là 2.

Bước 3: Ghi lại đa thức

Sắp xếp các hạng tử theo thứ tự giảm dần của mũ.

Ghi lại đa thức bằng cách kết hợp các hạng tử đã được sắp xếp và thêm dấu cộng (+) hoặc trừ (-) phù hợp giữa các hạng tử.

Ví dụ: Trong đa thức f(x) = 3x^2 - 5x + 2, ghi lại đa thức theo thứ tự giảm dần là 3x^2 - 5x + 2.

Bước 4: Ký hiệu biến

Đặt ký hiệu cho biến trong đa thức. Thông thường, biến được ký hiệu là x.

Ví dụ: Trong đa thức f(x) = 3x^2 - 5x + 2, biến được ký hiệu là x.

Khi đã hoàn thành các bước trên, chúng ta đã xác định được đa thức một biến. Ví dụ trên cho thấy đa thức f(x) = 3x^2 - 5x + 2 với biến x, có ba hạng tử và bậc là 2.

Các bước tiến hành giải một bài toán đa thức của một biến

Để giải bài toán ta có thể làm theo các bước sau:

Bước 1: Xác định mục tiêu của lời giải

Đọc hiểu cụ thể bài toán để xác định mục tiêu của lời giải. Bài toán có thể yêu cầu tìm giá trị của biến, tìm điểm cực trị, tìm nghiệm của phương trình đa thức hoặc thực hiện các phép toán khác trên đa thức.

Bước 2: Xác định phương pháp giải

Xác định phương pháp giải phù hợp dựa trên mục tiêu giải pháp. Có nhiều phương pháp giải đa thức với biến như biểu diễn đồ thị, phân tích bậc, sử dụng thuật toán chia đôi, sử dụng định lý Viét hoặc sử dụng các phương pháp đa thức khác.

Bước 3: Thực hiện phương pháp giải

Áp dụng phương pháp giải đã xác định cho đa thức cụ thể.Thực hiện các phép tính và thuật toán tương ứng để đạt được mục tiêu giải pháp.

Bước 4: Kiểm tra lại kết quả

Sau khi thực hiện xong cách giải, kiểm tra lại kết quả để đảm bảo độ chính xác. Chúng ta thường kiểm tra điều này bằng cách thay kết quả vào đa thức ban đầu và kiểm tra xem nó có đáp ứng yêu cầu của bài toán hay không.

Bước 5: Trình bày kết quả

Ghi kết quả cuối cùng theo yêu cầu của bài toán. Tùy thuộc vào mục tiêu của lời giải ban đầu, đây có thể là các giá trị thay đổi, điểm cực trị, nghiệm của phương trình đa thức hoặc các kết quả khác.

Quá trình giải một bài toán nó có thể phức tạp hoặc đơn giản tùy thuộc vào độ phức tạp của đa thức và yêu cầu của bài toán. Điều quan trọng nhất là phải hiểu rõ vấn đề và lựa chọn phương pháp giải quyết phù hợp để đạt được kết quả mong muốn.

Một số lưu ý khi giải đa thức của một biến

Khi giải đa thức cho một biến, dưới đây là một số lưu ý quan trọng:

• Đọc và hiểu bài toán: Đọc kỹ bài toán để hiểu yêu cầu của nó. Xác định câu hỏi và phương pháp giải pháp và mọi điều kiện hoặc hạn chế liên quan.
• Xác định phương pháp giải:Tùy theo mục tiêu giải pháp mà xác định phương pháp giải phù hợp.Có nhiều phương pháp giải đa thức như biểu diễn đồ thị, phân tích bậc, sử dụng thuật toán chia đôi, định lý Viét hoặc sử dụng các phương pháp đa thức khác.
• Kiểm tra tính hợp lệ của đa thức: Xác định xem đa thức có hợp lệ hay không. Đa thức hợp lệ là đa thức trong đó các số hạng và phép tính của đa thức được thực hiện chính xác.
• Phân tích bậc đa thức: Xác định bậc của đa thức bằng cách xem xét số mũ cao nhất của biến trong đa thức. Bậc của đa thức có thể ảnh hưởng đến phương pháp giải.
• Vẽ đồ thị đa thức: Vẽ đồ thị của đa thức trong hệ tọa độ để tìm kiếm những thông tin quan trọng như điểm cực trị, giao điểm trục hoành, giao điểm trục tung.
• Kiểm tra kết quả: Sau khi hoàn thành cách giải, kiểm tra kết quả bằng cách thay thế vào đa thức ban đầu và kiểm tra xem có đáp ứng yêu cầu của bài toán hay không.
• Trình bày kết quả: Ghi kết quả cuối cùng theo yêu cầu của bài toán. Đảm bảo sự rõ ràng và chính xác khi trình bày kết quả.
• Kiên nhẫn và chính xác: Việc giải đa thức theo một biến có thể đòi hỏi sự kiên nhẫn và cẩn thận. Duy trì độ chính xác khi thực hiện tính toán và làm theo các bước giải.

Bài tập áp dụng

• Bài tập 1:

Cho đa thức f(x) = 2x^3 - 5x^2 + 3x - 7. Hãy thực hiện các bước sau:

a) Xác định bậc của đa thức f(x).

b) Ghi lại đa thức f(x) theo thứ tự giảm dần của mũ.

c) Tìm giá trị của f(2).

Đáp án:

a) Bậc của đa thức f(x) là 3.

b) Ghi lại đa thức f(x) theo thứ tự giảm dần của mũ: 2x^3 - 5x^2 + 3x - 7.

c) Để tìm giá trị của f(2), thay x = 2 vào đa thức: f(2) = 2(2)^3 - 5(2)^2 + 3(2) - 7 = 8 - 20 + 6 - 7 = -13.

• Bài tập 2:

Cho đa thức f(x) = x^4 - 4x^3 + 5x^2 + 3x - 6. Hãy thực hiện các bước sau:

a) Xác định bậc của đa thức f(x).

b) Ghi lại đa thức f(x) theo thứ tự giảm dần của mũ.

c) Tìm các nghiệm của phương trình f(x) = 0.

Đáp án:

a) Bậc của đa thức f(x) là 4.

b) Ghi lại đa thức f(x) theo thứ tự giảm dần của mũ: x^4 - 4x^3 + 5x^2 + 3x - 6.

c) Để tìm các nghiệm của phương trình f(x) = 0, ta có thể sử dụng các phương pháp như phân tích bậc, đồ thị hóa, hoặc sử dụng các thuật toán giải phương trình đa thức. Kết quả sẽ phụ thuộc vào phương pháp sử dụng.

• Bài tập 3:

Cho đa thức f(x) = 3x^2 - 6x + 2. Hãy thực hiện các bước sau:

a) Xác định bậc của đa thức f(x).

b) Ghi lại đa thức f(x) theo thứ tự giảm dần của mũ.

c) Tìm các điểm cực trị của đa thức f(x).

Đáp án:

a) Bậc của đa thức f(x) là 2.

b) Ghi lại đa thức f(x) theo thứ tự giảm dần của mũ: 3x^2 - 6x + 2.

c) Để tìm các điểm cực trị của đa thức f(x), ta có thể sử dụng phương pháp đạo hàm. Đạo hàm của đa thức sẽ cho ta các điểm cực trị của đa thức. Từ đó, ta có thể xác định các điểm cực trị cụ thể.

• Bài tập 4:

Cho đa thức f(x) = 2x^3 - 7x^2 + 4x - 1. Hãy tìm tất cả các điểm cắt của đồ thị đa thức f(x) với trục hoành.

Đáp án:

Để tìm các điểm cắt của đồ thị đa thức f(x) với trục hoành, ta cần giải phương trình f(x) = 0. Trong trường hợp này, tìm nghiệm của phương trình 2x^3 - 7x^2 + 4x - 1 = 0 để xác định các điểm cắt. Để giải phương trình này, bạn có thể sử dụng các phương pháp như phân tích bậc, sử dụng định lý Viét, hoặc sử dụng các thuật toán giải phương trình đa thức. Kết quả sẽ phụ thuộc vào phương pháp sử dụng.

• Bài tập 5:

Cho đa thức f(x) = x^3 + 2x^2 + x + 1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của đa thức trên đoạn [0, 1].

Đáp án:

Để tìm giá trị lớn nhất và giá trị nhỏ nhất của đa thức trên đoạn [0, 1], ta cần tìm điểm cực trị của đa thức và so sánh giá trị của đa thức tại các điểm cực trị và đầu mút đoạn. Để tìm điểm cực trị, ta có thể sử dụng phương pháp đạo hàm. Tính giá trị của đa thức tại các điểm cực trị và đầu mút đoạn, sau đó so sánh để tìm giá trị lớn nhất và giá trị nhỏ nhất.

Kết luận

Hy vọng rằng những bài tập trên đã giúp bạn ôn tập và nắm vững hơn về cách giải quyết các bài toán liên quan đến đa thức. Đa thức một biến là một phần quan trọng trong toán học và có nhiều ứng dụng trong thực tế. Bằng cách thực hành giải các bài tập, bạn có thể rèn luyện khả năng phân tích và xử lý các đa thức phức tạp.