Công thức tính lãi kép và các dạng bài tập thường gặp

Lý thuyết, công thức tính lãi kép cùng các dạng bài tập thường hay xuất hiện nhất trong các đề thi. Đi kèm hướng dẫn giải chi tiết và dễ hiểu nhất.

Tổng hợp lý thuyết, công thức tính lãi kép và các dạng bài tập thường gặp trong các đề thi. Bài viết dưới đây của thayphu trình bày đầy đủ về phương pháp giải, ví dụ minh họa và lời giải chi tiết nhất cho các em tham khảo!

Lý thuyết về lãi kép và công thức tính lãi kép

Lý thuyết và công thức tính lãi kép

Nếu đến kỳ hạn người gửi tiết kiệm không rút lãi ra thì tiền lãi được tính vào vốn của kỳ kế tiếp.

Công thức tính lãi kép:

Khách hàng gửi vào ngân hàng A đồng với lãi kép là r% /kỳ hạn thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n kỳ hạn (n thuộc N*) sẽ là:

Sn = A(1 + r)^n (2)

Lưu ý: Với công thức (2) ta có thể suy ra: n = log (1+r) (Sn/A) (3)

r% = nSn/A - 1 (4)

A = Sn / (1+r)^n (5)

Một số dạng toán liên quan đến lãi kép

Dạng 1 - Bài toán tiết kiệm (Thể thức lãi kép không có kỳ hạn)

Khách hàng gửi vào ngân hàng số tiền là A đồng, lãi suất r% mỗi tháng theo hình thức lãi kép và gửi theo phương thức không kỳ hạn. Đề bài yêu cầu tính số tiền cả vốn lẫn lãi mà khách hàng nhận được sau N tháng.

Phương pháp giải:

Gọi TN là số tiền cả vốn lẫn lãi sau N tháng, ta có:

• Sau 1 tháng (k = 1): T1 = A + A.r = A(1 + r)
• Sau 2 tháng (k = 2: T2 = A(1 + r) + A (1 + r).r = A(1 + r)^2
• Cứ như vậy sau N tháng (k = N): TN = A(1 + r)^N

Vậy số tiền cả vốn lẫn lãi khách hàng có được sau N tháng sẽ là: TN = A(1 + r)^N

Lưu ý: Lãi suất thường được cho ở dạng a% nên khi tính toán các em phải tính r = a : 100 rồi mới thay thế vào công thức.

Các bài tập liên quan đến lãi suất kép

Bài tập 1: Anh Hòa gửi vào ngân hàng 10 triệu đồng với lãi kép là 5%/năm. Hãy tính số tiền cả gốc lẫn lãi mà anh Hòa nhận lại sau khi gửi ngân hàng 10 năm?

Giải:

Số tiền cả gốc lẫn lãi anh Hòa nhận được sau 10 năm với lãi kép 5%/năm là:

S10 = 10.(1 + 5/100)^10 = 16,2888 triệu đồng.

Kết luận sau 10 năm anh Hòa nhận được số tiền cả gốc lẫn lãi là khoảng 16,2888 triệu đồng.

Bài tập 2: Chị Lan gửi vào ngân hàng 10 triệu đồng. Với số tiền đó nếu chị Lan gửi với lãi kép 5/12% /tháng thì sau 10 năm chị Lan nhận được bao nhiêu tiền?

Giải:

Ta có: 10 năm = 12.10 = 120 tháng

Số tiền cả gốc lẫn lãi nhận được sau 10 năm với lãi kép 5/12% / tháng là:

S120 = 10. (1 + 5/(12 x 100))^120 = 16, 4700 triệu đồng.

Vậy sau 10 năm chị Lan sẽ nhận được số tiền là khoảng 16, 4700 triệu đồng.

Dạng 2 - Thể thức lãi kép có kỳ hạn

Khách hàng gửi vào ngân hàng số tiền là A đồng, lãi suất r% mỗi tháng theo hình thức lãi kép, gửi theo phương thức có kỳ hạn m tháng. Yêu cầu tính số tiền cả vốn lẫn lãi mà người đó nhận được sau N kỳ hạn?

Phương pháp giải:

Dạng này cũng tương tự như dạng 1 nhưng các em sẽ đi tính lãi suất theo định kỳ m tháng là r’ = m.r.

Sau đó sử dụng công thức TN = A(1 + r’)^N với N là số kỳ hạn.

Lưu ý: Trong cùng 1 kỳ hạn, lãi suất sẽ giống nhau mà không được cộng vào vốn để tính lãi kép.

Bài tập 1: Bác An gửi tiết kiệm 100 triệu vào ngân hàng theo mức kỳ hạn 6 tháng với lãi suất là 0.65% mỗi tháng. Hỏi sau 10 năm, số tiền cả vốn lẫn lãi mà bác An nhận được là bao nhiêu? Biết rằng trong 10 năm bác không rút số tiền đó.

Giải:

Số kỳ hạn N = (10.12)/6 = 20 kỳ hạn

Lãi suất theo định kỳ 6 tháng là 6.0,65% = 3,9%

Số tiền cả vốn lẫn lãi mà bác An nhận được sau 10 năm là:

T = 100 (1 + 3,9%)^20 = 214,9 triệu đồng

Vậy số tiền bác An nhận được là 214,9 triệu đồng.

Bài tập 2: Bạn Liên gửi tiết kiệm số tiền là 50 triệu đồng với lãi suất 0,79% /tháng theo phương thức lãi kép. Hãy tính số tiền mà bạn Liên nhận được sau 2 năm?

Giải:

Đây là bài toán lãi kép với chu kỳ là một tháng nên áp dụng công thức TN = A(1 + r’)^N

Ta có: A = 50 triệu đồng, r% = 0,79% và N = 2.12 = 24 tháng.

Số tiền cả gốc lẫn lãi mà bạn Liên nhận được sau 2 năm sẽ là:

TN = 50.(1 + 0,0079)^24 = 60,393 triệu đồng.

Dạng 3 - Bài toán tính lũy hàng tháng/quý/năm gửi một số tiền cố định vào ngân hàng

Khách hàng gửi vào ngân hàng số tiền A đồng mỗi tháng với lãi suất mỗi tháng là r. Hỏi sau N tháng, người đó có tất cả bao nhiêu tiền?

Phương pháp giải:

Gọi TN là số tiền có được sau N tháng

• Cuối tháng thứ 1: T1 = A (1 + r)
• Đầu tháng thứ 2: A(1 + r) + A = A/r [(1 + r)^2 -1]
• Cuối tháng thứ 2: T2 = A/r [(1+r)^2 -1] + A/r[(1+r)^2 -1].r

= A/r[(1+r)^2 -1] (1+r)

• Đầu tháng thứ N: A/r[(1+r)^N -1]
• Cuối tháng thứ N: TN = A/r[(1+r)^N -1] (1+r)

Vậy sau N tháng số tiền vốn lẫn lãi khách hàng có được là:

TN = A/r[(1+r)^N -1](1+r)

Bài tập 1:Theo hình thức lãi kép, đầu mỗi tháng chị Hiền gửi đều đặn vào ngân hàng số tiền là 10 triệu đồng. Lãi suất theo kỳ hạn 1 tháng là 0.5%. Hỏi sau 2 năm số tiền chị Hiền nhận được là bao nhiêu?

Giải:

Sau 2 năm chị Hiền thu được số tiền là:

10(1 + 0,005)^24 + 10(1 + 0,005)^23 + … + 10(1 + 0,005)^1

= 10(1 + 0,005). ((1 + 0,005)^24 -1))/0,005 = 255, 591 triệu đồng

Bài tập 2: Anh Tiến đều đặn mỗi tháng đều gửi vào ngân hàng một khoản tiền tiết kiệm là x đồng. Tìm x để người này nhận về số tiền 200 triệu đồng sau 36 tháng gửi tiết kiệm. Biết rằng tiền gửi theo hình thức lãi suất kép, kỳ hạn lãi suất 1 tháng là 0,67% và lãi suất không đổi trong thời gian gửi.

Giải:

Tổng số tiền nhận được là:

x(1+0,0067)^36 + x(1+0,0067)^35 +... +x(1+0,0067)^1 = 200.10^6

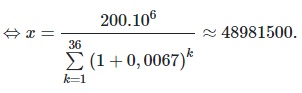
Bài viết vừa tổng hợp đầy đủ nhất về công thức tính lãi kép và các dạng bài tập liên quan. Chúc các em có những phút giây học tập tốt và đạt điểm cao trong các kỳ thi sắp tới nhé!