Chu vi hình tứ giác là gì? Cách tính và ví dụ cụ thể

Cách tính chu vi tứ giác phụ thuộc vào loại hình tứ giác và thông tin có sẵn về các đoạn thẳng trong hình. Dưới đây là một số cách tính và định nghĩa.

Chu vi của một hình tứ giác giúp chúng ta hiểu và mô tả độ dài các cạnh xung quanh hình đó, đồng thời cung cấp những thông tin quan trọng về hình dạng và kích thước của hình đó.Trong bài viết này của thayphu sẽ khảo sát các phương pháp tính chu vi tứ giác đối với các loại tứ giác lồi và lõm khác nhau.

Khái niệm về chu vi hình tứ giác

Khái niệm về chu vi hình tứ giác

Chu vi của một hình tứ giác là tổng độ dài các cạnh của hình này. Chu vi được sử dụng để đo chiều dài của cạnh xung quanh một hình tứ giác và cung cấp cho chúng ta thông tin về kích thước cũng như hình dạng của nó. Đối với một tứ giác lồi, chu vi được tính bằng cách cộng tổng chiều dài mỗi cạnh.

Đối với một tứ giác lõm, chu vi cũng được tính bằng cách cộng độ dài các cạnh. Tuy nhiên, có thể xảy ra trường hợp cạnh đi qua một khoảng trống trong hình.

Để tính chu vi của một hình tứ giác, chúng ta cần biết độ dài các cạnh hoặc các thông tin liên quan như đường chéo, góc xen giữa các cạnh hoặc các thông tin khác về hình dạng.

Tính chất của chu vi hình tứ giác

Nó có một số tính chất quan trọng. Dưới đây là một số tính chất cơ bản về chu vi của một hình tứ giác:

• Tính chất chung: Chu vi của một hình tứ giác là tổng độ dài các cạnh của hình đó. Điều này áp dụng cho cả tứ giác lồi và lõm.
• Tính chất đối xứng: Chu vi của một tứ giác không thay đổi nếu ta đổi vị trí các cạnh tương ứng. Điều này có nghĩa là nếu chúng ta đổi chỗ hai cạnh của một tứ giác thì chu vi vẫn không đổi.
• Tính đồng nhất: Trong một tứ giác lồi, chu vi đạt giá trị nhỏ nhất khi các cạnh của hình đó bằng nhau. Đối với một tứ giác lõm, chu vi có thể đạt giá trị nhỏ nhất khi một số cạnh có độ dài bằng 0 và tạo thành đỉnh của tứ giác.
• Tính chất vô hướng: Chu vi của một tứ giác không phụ thuộc vào thứ tự đo các cạnh. Điều này có nghĩa là việc tính chu vi theo thứ tự bất kỳ sẽ cho kết quả như nhau.
• Tính chất cộng: Chu vi của một tứ giác có thể được tính bằng cách cộng tổng độ dài các cạnh hoặc cộng các đoạn thẳng không cắt nhau ở cạnh của hình đó.

Công thức tính chu vi hình tứ giác

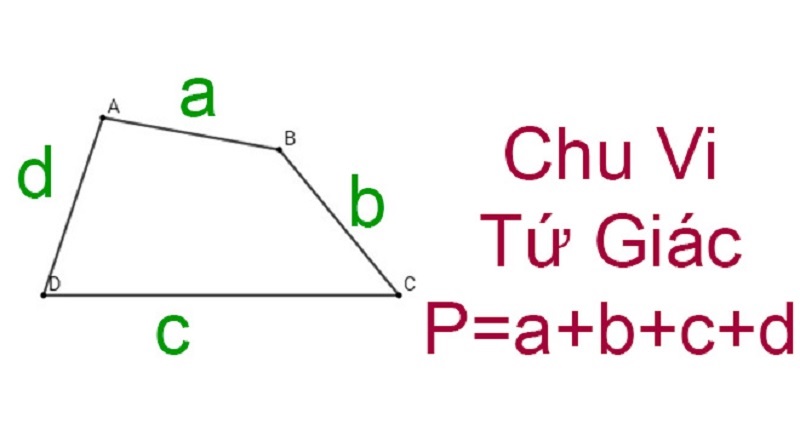
Công thức tính chu vi hình tứ giác

Công thức tính chu vi của một hình tứ giác phụ thuộc vào loại hình tứ giác và thông tin có sẵn về các đoạn thẳng trong hình. Dưới đây là các công thức tính chu vi cho một số loại hình tứ giác phổ biến:

Hình tứ giác lồi (hình tứ giác bất kỳ)

Chu vi (P) = a + b + c + d

Trong đó, a, b, c, d lần lượt là độ dài các cạnh của hình tứ giác.

Hình tứ giác vuông

Chu vi (P) = a + b + c + d

Trong đó, a, b, c, d lần lượt là độ dài các cạnh của hình tứ giác vuông.

Hình tứ giác chữ nhật

Chu vi (P) = 2a + 2b

Trong đó, a và b lần lượt là độ dài hai cạnh kề của hình tứ giác chữ nhật.

Hình tứ giác bình phương

Chu vi (P) = 4a

Trong đó, a là độ dài cạnh của hình tứ giác bình phương.

Các công thức trên đề cập đến một số loại hình tứ giác phổ biến, tuy nhiên, có thể có các công thức khác cho các loại hình tứ giác đặc biệt khác. Để tính chu vi của một hình tứ giác cụ thể, ta cần biết độ dài các cạnh hoặc các thông tin liên quan khác về hình dạng của nó.

Một số dạng toán về chu vi hình tứ giác

Dưới đây là một số dạng toán phổ biến liên quan đến chu vi của một tứ giác:

Tìm chu vi của tứ giác

Trong dạng toán này, bạn được cho chiều dài các cạnh của tứ giác và bài toán. Nhiệm vụ là tính toán phạm vi của nó. Bạn có thể áp dụng các công thức trên để giải quyết vấn đề này.

Tính độ dài các cạnh của một hình tứ giác

Trong trường hợp này bạn đã biết chu vi của hình tứ giác đó và một số thông tin về độ dài của các cạnh.Nhiệm vụ của bạn là tìm độ dài các cạnh chưa biết. Để giải bài toán này, bạn có thể sử dụng hệ phương trình để tìm các giá trị cần tìm.

Bài tập so sánh chu vi

Trong bài tập này, bạn được giao hai hình vuông và yêu cầu so sánh chu vi của chúng. Bạn cần tính chu vi của mỗi hình tứ giác và so sánh kết quả để xác định hình nào có chu vi lớn nhất.

Kỹ thuật định vị

Trong một số trường hợp, bạn có thể thấy một số đoạn thẳng hoặc chéo trong một hình vuông và được yêu cầu xác định độ dài cạnh hoặc chu vi của hình đó. Bài toán này yêu cầu bạn áp dụng các quy tắc hình học và sử dụng kiến thức về tỷ lệ, định lý Pythagore hoặc định luật cosin để giải.

Bài tập áp dụng

Bài 1:Chu vi của một hình tứ giác lồi có các cạnh lần lượt là 5 cm, 8 cm, 6cm và 7cm là:

a) 20 cm

b) 26 cm

c) 32 cm

d) 36 cm

Đáp án: c) 32 cm

Bài 2: Hình tứ giác ABCD là hình tứ giác vuông, với các cạnh lần lượt là 6 cm, 8 cm, 10 cm và 7 cm. Chu vi của hình tứ giác là:

a) 22 cm

b) 28 cm

c) 32 cm

d) 34 cm

Đáp án: b) 28 cm

Bài 3: Hình tứ giác ABCD là hình tứ giác chữ nhật với chiều dài là 10 cm và chiều rộng là 6 cm. Chu vi của hình tứ giác là:

a) 20 cm

b) 24 cm

c) 26 cm

d) 30 cm

Đáp án: b) 24 cm

Bài 4: Hình tứ giác ABCD là hình tứ giác bình phương với cạnh là 5 cm. Chu vi của hình tứ giác là:

a) 15 cm

b) 20 cm

c) 25 cm

d) 30 cm

Đáp án: b) 20 cm

Bài 5: Hình tứ giác ABCD có các cạnh lần lượt là a, 2a, a + 3 và 4a - 1. Chu vi của hình tứ giác là:

a) 10a + 2

b) 12a + 2

c) 14a + 2

d) 16a + 2

Đáp án: c) 14a + 2

Bài 6: Hình tứ giác ABCD là hình tứ giác lồi có chu vi là 28 cm. Nếu độ dài cạnh AD là 8 cm, chu vi của hình tứ giác sau khi cắt bỏ cạnh AD là:

a) 10 cm

b) 12 cm

c) 14 cm

d) 16 cm

Đáp án: b) 12 cm

Bài 7: Hình tứ giác ABCD là hình tứ giác lồi có chu vi là P. Nếu tăng độ dài của mỗi cạnh lên gấp đôi, chu vi của hình tứ giác mới là:

a) P

b) 2P

c) 3P

d) 4P

Đáp án: b) 2P

Bài 8: Hình tứ giác ABCD là hình tứ giác lồi có chu vi là 36 cm. Nếu các cạnh AB và CD bằng nhau, chu vi của hình tứ giác sau khi cắt bỏ hai cạnh này là:

a) 12 cm

b) 18 cm

c) 24 cm

d) 30 cm

Đáp án: c) 24 cm

Bài 9: Hình tứ giác ABCD là hình tứ giác lồi có chu vi là 40 cm. Nếu cạnh AB là 10 cm và cạnh CD là 12 cm, chu vi của hình tứ giác sau khi tăng độ dài cạnh AB lên gấp đôi là:

a) 42 cm

b) 44 cm

c) 46 cm

d) 48 cm

Đáp án: b) 44 cm

Bài 10: Hình tứ giác ABCD là hình tứ giác lồi có chu vi là 50 cm. Nếu tăng độ dài của mỗi cạnh lên 3 lần, chu vi của hình tứ giác mới là:

a) 150 cm

b) 160 cm

c) 170 cm

d) 180

Đáp án: a) 150 cm

Kết luận

Trên đây là những thông tin về cách tính chu vi hình tứ giác hi vọng những thông tin giúp bạn nắm vững kiến thức hơn về vấn đề này.