Chu vi hình thoi, tổng hợp công thức và các quy tắc tính

Chu vi hình thoi là tổng độ dài của tất cả các cạnh của hình thoi đó. Trong một hình thoi, cạnh đối diện nhau có độ dài bằng nhau và bằng 4xa.

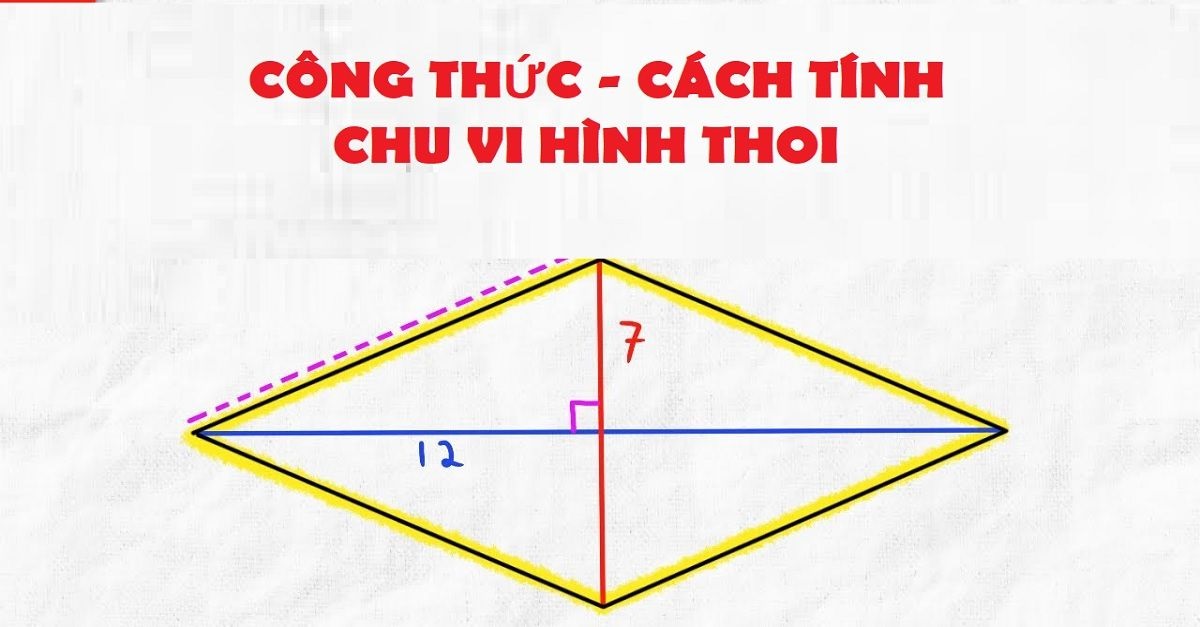
Tổng hợp những công thức cách tính chu vi hình thoi

Trong hình học,hình thoi là một hình dạng độc đáo với những tính chất đặc biệt. Một trong những khía cạnh quan trọng của hình thoi là chu vi hình thoi, một đại lượng quan trọng giúp chúng ta hiểu và xác định chiều dài của hình thoi. Trong bài viết này của thayphu chúng ta sẽ xem xét chu vi của hình thoi và tìm hiểu cách tính chu vi của nó cũng như các công thức liên quan.

Chu vi hình thoi hay còn được gọi là chu vi gì?

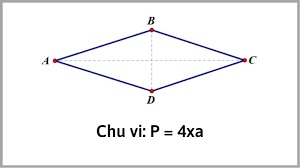
Chu vi hình thoi hay còn được gọi là chu vi gì

Chu vi hình thoi, còn gọi là chu vi của hình thoi,là một khái niệm quan trọng trong hình học. Chu vi biểu thị tổng chiều dài của tất cả các cạnh của hình thoi, là thông số quan trọng để đo và xác định kích thước của hình thoi.

Chu vi của hình thoi là một khái niệm quan trọng trong nhiều lĩnh vực, bao gồm công nghệ, kiến trúc và thiết kế. Nó cung cấp thông tin về kích thước và tỷ lệ của hình thoi và cho phép chúng ta đo lường, tính toán và áp dụng nó vào các vấn đề trong thế giới thực.Việc hiểu và áp dụng chu vi hình thoi không chỉ giúp chúng ta học những kiến thức hình học cơ bản mà còn mở ra cánh cửa khám phá sâu hơn về các dạng và phương pháp tính toán.

Tính chất của chu vi hình thoi

Chu vi của hình thoi có một số tính chất đáng chú ý, bao gồm:

Các cạnh đối diện của hình thoi có chiều dài bằng nhau

Điều này có nghĩa là nếu hai cạnh của hình thoi bằng nhau thì bốn cạnh đối diện cũng bằng nhau và cùng chiều dài.Đây là một tính chất quan trọng của hình thoi và đảm bảo tính đối xứng và đẳng giác của hình thoi.

Tổng chiều dài các cạnh của hình thoi

Chu vi của hình thoi là tổng độ dài các cạnh của nó.Với một cạnh của hình thoi có chiều dài a,chu vi (P) của hình thoi được tính theo công thức P = 4a.

Mối quan hệ giữa chu vi và đường kính

Trong hình thoi, đường kính là đường thẳng đi qua tâm của hai đỉnh kề nhau. Chu vi của hình thoi có thể được tính bằng cách nhân đường kính (d) với một hệ số nhất định. Công thức này là P = 2d, trong đó d là chiều dài đường kính của viên kim cương.

Tính chất bên trong của tam giác

Một hình thoi có thể chia thành hai tam giác đều bằng một đường chéo. Điều này có nghĩa là chu vi của hình thoi có thể được tính bằng tổng độ dài các cạnh của hai tam giác này.

Những quy tắc tính chu vi hình thoi

Để tính chu vi hình thoi, chúng ta có thể áp dụng các quy tắc và công thức sau:

Chu vi hình thoi có cạnh (a)

Chu vi (P) = 4 * a. Đây là công thức đơn giản nhất để tính chu vi hình thoi khi biết độ dài một cạnh.

Chu vi hình thoi có đường kính (d)

Chu vi (P) = 2 * d.Nếu biết đường kính của hình thoi,chúng ta có thể tính chu vi bằng cách nhân đường kính với 2.

Chu vi hình thoi có cạnh và góc

Cho độ dài một cạnh (a) và góc ( θ) giữa hai cạnh kề nhau, ta có thể tính chu vi hình thoi theo công thức P = 2 * a * cos( θ). Trong trường hợp đặc biệt khi góc θ là 90 độ, công thức là P = 2 * a * sqrt(2), trong đó sqrt là ký hiệu căn bậc hai.

Chu vi hình thoi có đường chéo (d1, d2)

Nếu biết độ dài hai đường chéo của hình thoi (d1 và d2), chúng ta có thể tính chu vi bằng công thức P = 2 * sqrt(d1^2 + d2^ 2) . Đây là công thức Pythagore được áp dụng trong trường hợp này.

Tổng hợp công thức tính chu vi hình thoi

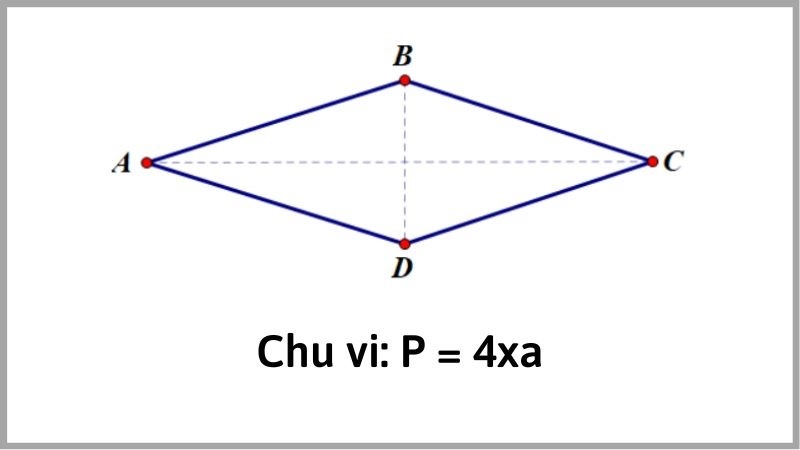
Tổng hợp công thức tính chu vi hình thoi

Dưới đây thayphu đã tổng hợp những công thức tính chu vi hình thoi mà bạn có thể tham khảo

Công thức tính chu vi hình thoi

Chu vi của hình thoi được tính bằng cách nhân chiều dài của cạnh kim cương với số 4, vì tất cả các cạnh của viên kim cương đều có cùng chiều dài.

Công thức tính chu vi của hình thoi là:

P = 4 * a

Trong đó P là chu vi hình thoi và a là chiều dài một cạnh của hình thoi.

Đây là công thức đơn giản nhất để tính chu vi hình thoi. Nếu biết độ dài một cạnh, chúng ta chỉ cần nhân nó với 4 để tính chu vi.

Công thức tính chu vi hình thoi lớp 4

Ở lớp 4, công thức cơ bản để tính chu vi hình thoi là:

Chu vi (P) của hình thoi = 2 * (đường dọc + đường ngang)

Đường thẳng dọc và đường ngang là độ dài hai cạnh kề nhau của hình thoi.

Ví dụ: Nếu đường thẳng đứng của hình thoi có kích thước 5 đơn vị và đường ngang có kích thước 8 đơn vị thì chúng ta có thể tính chu vi như sau:

P = 2 * (5 + 8) = 2 * 13 = 26

Do đó, chu vi là hình thoi trong trường hợp này là 26 đơn vị.

Công thức tính chu vi của hình thoi lớp 5

Ở lớp 5, công thức cơ bản để tính chu vi của hình thoi là:

Chu vi (P) của hình thoi = 4 * Độ dài cạnh

Đây là công thức tính chu vi của hình thoi đơn giản nhất. Chúng ta chỉ cần nhân chiều dài một cạnh với số 4 để tính chu vi.

Ví dụ: Nếu chiều dài cạnh của hình thoi là 6 đơn vị, chúng ta có thể tính chu vi như sau:

P = 4 * 6 = 24

Do đó, chu vi của hình thoi trong trường hợp này là 24 đơn vị.

Cách tìm cạnh để tính chu vi của hình thoi

Để tính chu vi của hình thoi, bạn có thể tìm độ dài cạnh như sau:

Biết chu vi

Nếu biết chu vi của hình thoi, bạn có thể sử dụng công thức P = 4 * a. Trong đó P là chu vi và a là chiều dài cạnh. Bạn có thể sử dụng công thức này để giải phương trình tìm giá trị của a.

Biết đường kính

Nếu biết đường kính của hình thoi (đường đi qua trung điểm của hai cạnh kề nhau) thì có thể sử dụng công thức P = 2 * d, trong đó P là chu vi và d là đường kính .Bạn có thể sử dụng công thức này để giải phương trình tìm giá trị của d. Sau đó, bạn có thể tính chiều dài cạnh bằng một nửa đường kính.

Biết diện tích

Nếu biết diện tích hình thoi, bạn có thể sử dụng công thức S = a^2 * sin(θ), trong đó S là diện tích, a là độ dài cạnh và θ là góc giữa hai trang liền kề. Bạn có thể sử dụng công thức này để giải phương trình tìm giá trị của a.

Công thức nâng cao tính chu vi hình thoi

Có một số công thức nâng cao hơn để tính chu vi của hình thoi, đặc biệt khi chúng ta có thông tin hạn chế. Dưới đây là một số công thức thông dụng:

• Biết độ dài một cạnh (a): Chu vi (P) = 4 * a. Đây là công thức cơ bản nhất và được sử dụng khi chúng ta biết chiều dài một cạnh của hình thoi.
• Biết đường kính (d): Chu vi (P) = 2 * d. Nếu chỉ biết đường kính của hình thoi (đường đi qua trung điểm của hai cạnh kề nhau) thì chúng ta có thể tính chu vi bằng cách nhân đường kính với 2.
• Biết độ dài đường chéo (d1, d2 ): Chu vi (P) = 2 * Căn bậc hai (d1^2 + d2^2). Nếu chỉ biết độ dài hai đường chéo của hình thoi (d1 và d2), chúng ta có thể tính chu vi bằng công thức Pythagore.
• Biết diện tích (S): chu vi (P) = 2 * sqrt(2 * S). Nếu chỉ biết diện tích hình thoi thì chúng ta có thể sử dụng công thức để tính chu vi.
• Biết một cạnh và một góc (a, θ): Chu vi (P) = 2 * a * cos(θ).Nếu biết độ dài một cạnh (a) và góc (θ) giữa hai cạnh kề nhau, chúng ta có thể sử dụng công thức để tính chu vi.

Cách chứng minh chu vi hình thoi

Để chứng minh rằng tổng độ dài các cạnh của hình thoi bằng nhau, chúng ta có thể sử dụng một số phương pháp chứng minh hình học. Đây là một cách để chứng minh điều này bằng cách sử dụng các phương trình và tính chất của hình thoi:

Chứng minh:Xét hình thoi ABCD có các cạnh lần lượt là AB, BC, CD và DA.

Bước 1: Chứng minh AB = CD

Sử dụng tính chất của hình thoi, ta biết các đường chéo của hình thoi cắt nhau theo phương thẳng đứng và chia đôi nhau. Do đó đường chéo AC chia AB thành hai phần bằng nhau.

Tương tự, đường chéo AC cũng chia CD thành hai phần bằng nhau.

Vì đường chéo AC chia AB và CD thành hai phần bằng nhau và song song nên AB = CD.

Bước 2: Chứng minh BC = DA.

Áp dụng tính chất của hình thoi thì biết các cạnh của hình thoi bằng nhau.

Do đó BC = AB và DA = CD.- Vì AB = CD (chứng minh ở bước 1) nên BC = DA.

Hai phép thử ở bước 1 và bước 2 cho kết quả AB = CD và BC = DA. Tổng hợp hai phương trình này ta được:

AB + BC + CD + DA = CD + DA + BC + AB = CD + AB + BC + DA

Vì AB = CD và BC = DA nên:

AB + BC + CD + DA = AB + BC + AB + BC = 2(AB + BC)

Cuối cùng, ta kết luận rằng chu vi của hình thoi bằng nhau:

AB + BC + CD + DA = 2(AB + BC )

Do đó, tổng độ dài các cạnh của hình thoi bằng nhau và điều này chứng tỏ chu vi của hình thoi không đổi.

Bài tập áp dụng

Bài tập 1:

Hình thoi ABCD có độ dài cạnh AB là 6 cm. Hãy tính chu vi của hình thoi này.

Đáp án:

Chu vi của hình thoi là P = 4 * AB = 4 * 6 cm = 24 cm.

Bài tập 2:

Hình thoi ABCD có chu vi là 40 cm. Biết rằng độ dài một đường chéo của hình thoi là 16 cm. Hãy tính độ dài cạnh của hình thoi.

Đáp án:

Theo công thức chu vi hình thoi, ta có 40 cm = 4 * a, với a là độ dài cạnh của hình thoi.

Suy ra, a = 40 cm / 4 = 10 cm.

Bài tập 3:

Hình thoi ABCD có chu vi là 28 cm và đường kính là 12 cm. Hãy tính độ dài cạnh của hình thoi.

Đáp án:

Theo công thức chu vi hình thoi, ta có 28 cm = 2 * d, với d là đường kính của hình thoi.

Suy ra, d = 28 cm / 2 = 14 cm.

Độ dài cạnh của hình thoi là một nửa của đường kính, vậy cạnh của hình thoi là 14 cm / 2 = 7 cm.

Bài tập 4:

Hình thoi ABCD có chu vi là 36 cm. Biết rằng độ dài một cạnh là 10 cm và góc giữa hai cạnh kề nhau là 60 độ. Hãy tính độ dài đường chéo của hình thoi.

Đáp án:

Theo công thức chu vi hình thoi, ta có 36 cm = 2 * a * cos(θ), với a là độ dài cạnh và θ là góc giữa hai cạnh kề nhau.

Suy ra, cos(60 độ) = 36 cm / (2 * 10 cm) = 1/3.

Vậy a * (1/3) = 10 cm, suy ra a = 30 cm.

Đường chéo của hình thoi chính là đường kính, vậy độ dài đường chéo là 2 * a = 2 * 30 cm = 60 cm.

Bài tập 5:

Hình thoi ABCD có chu vi là 48 cm và diện tích là 64 cm^2. Hãy tính độ dài đường kính của hình thoi.

Đáp án:

Theo công thức chu vi hình thoi, ta có 48 cm = 2 * sqrt(2 * S), với S là diện tích của hình thoi.

Suy ra, sqrt(2 * S) = 48 cm / 2 = 24 cm.

Vậy 2 * S = (24 cm)^2 = 576 cm^2.

S = 576 cm^2 / 2 = 288 cm^2.

Diện tích của hình thoi là S = (đường kính)^2 / 2.

Suy ra, (đường kính)^2 = 2 * S = 2 * 288 cm^2 = 576 cm^2.

Vậy đường kính của hình thoi là sqrt(576 cm^2) = 24 cm.

Bài tập 6:

Hình thoi ABCD có chu vi là 60 cm và đường chéo chia một cạnh thành hai phần bằng nhau. Hãy tính độ dài cạnh của hình thoi.

Đáp án:

Vì đường chéo chia một cạnh thành hai phần bằng nhau, ta có AB = CD.

Chu vi của hình thoi là 60 cm = AB + BC + CD + DA = AB + BC + AB + BC = 2 * (AB + BC).

Suy ra, AB + BC =30 cm.

Vì AB = CD, ta có AB + BC + AB + BC = 2 * AB + 2 * BC = 30 cm.

Suy ra, AB + BC = 15 cm.

Vì AB = BC (do đường chéo chia một cạnh thành hai phần bằng nhau), ta có 2 * AB = 15 cm.

Suy ra, AB = 15 cm / 2 = 7.5 cm.

Vậy độ dài cạnh của hình thoi là 7.5 cm.

Bài tập 7:

Hình thoi ABCD có chu vi là 36 cm và độ dài một cạnh là 7 cm. Hãy tính độ dài đường chéo của hình thoi.

Đáp án:

Chu vi của hình thoi là 36 cm = 4 * a, với a là độ dài cạnh của hình thoi.

Suy ra, a = 36 cm / 4 = 9 cm.

Đường chéo của hình thoi chính là đường kính, vậy độ dài đường chéo là 2 * a = 2 * 9 cm = 18 cm.

Bài tập 8:

Hình thoi ABCD có diện tích là 100 cm^2 và góc giữa hai cạnh kề nhau là 45 độ. Hãy tính chu vi của hình thoi.

Đáp án:

Theo công thức chu vi hình thoi, ta có chu vi P = 2 * a * cos(θ), với a là độ dài cạnh và θ là góc giữa hai cạnh kề nhau.

Trong trường hợp này, góc giữa hai cạnh kề nhau là 45 độ, ta có cos(45 độ) = 1/√2 ≈ 0.707.

Với diện tích của hình thoi là 100 cm^2, ta có a^2 = 4 * S = 4 * 100 cm^2 = 400 cm^2.

Suy ra, a = √400 cm^2 = 20 cm.

Vậy chu vi của hình thoi là P = 2 * 20 cm * 0.707 ≈ 28.28 cm.

Thayphu.net hy vọng rằng các bài tập trước đã giúp bạn hiểu rõ hơn về chu vi của hình thoi và các phép tính liên quan. Khi hoàn thành các bài tập này, bạn có thể rèn luyện kỹ năng tính toán và áp dụng các công thức để giải các bài toán liên quan đến chu vi của hình thoi.