Cách tính chu vi hình thang, tổng hợp công thức và bài tạp

Cách tính chu vi hình thang khi biết các cạnh và các tính chất, định nghĩa, tính chất, công thức tính chu vi hình thang và các phương pháp.

Hình thang là một hình học rất phổ biến và xuất hiện thường xuyên trong các bài toán toán học và thực tế. Để giải các bài toán liên quan đến hình thang, việc tính chu vi của chúng là yêu cầu cơ bản. Chu vi của hình thang cung cấp thông tin quan trọng về độ dài của đường viền của hình và giúp chúng ta hiểu rõ hơn về hình dạng và đặc tính của nó.

Trong bài viết này, chúng ta sẽ cùng thayphu học cách tính chu vi hình thang và áp dụng các công thức thích hợp để có kết quả chính xác.

Chu vi hình thang được mọi người hiểu như thế nào

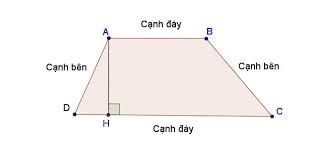
Chu vi hình thang được mọi người hiểu như thế nào

Chu vi của hình thang là độ dài toàn bộ cạnh của hình. Nó biểu thị tổng các cạnh của một hình thang, khi tính chu vi hình thang ta cần xác định các cạnh và các đoạn thẳng liên quan đến hình thang đó. Người ta hiểu chu vi hình thang là một khái niệm đơn giản và cơ bản trong hình học.

Cách tính chu vi hình thang là thước đo tổng quát về chiều dài của hình thang và được sử dụng rộng rãi trong các lĩnh vực như xây dựng, kiến trúc, thiết kế, toán học và các lĩnh vực liên quan khác.

Dấu hiệu nhận biết chu vi của một hình thang đặc biệt

Để xác định chu vi của hình thang, bạn có thể tìm hiểu từ các dấu hiệu và thông tin về hình thang này. Dưới đây là một số dấu hiệu để nhận biết chu vi hình thang:

• Cạnh: Hình thang có bốn cạnh, hai cạnh đối diện song song. Nếu bạn có thông tin về độ dài các cạnh, bạn có thể sử dụng công thức để tính chu vi hình thang.
• Góc: Hình thang có hai góc đối diện bằng nhau và hai góc còn lại cũng bằng nhau. Nếu biết giá trị của các góc, bạn có thể áp dụng các quy tắc hình học hoặc công thức góc để tính chu vi.
• Chiều cao: Chiều cao của hình thang là đoạn thẳng nối hai đỉnh không kề nhau của hình thang. Nếu bạn biết kinh độ của độ cao, bạn có thể sử dụng nó cùng với các cạnh và góc để tính chu vi.
• Tính đối xứng: Hình thang có trục đối xứng đi qua tâm hai cạnh đáy. Nếu bạn có thông tin về tính đối xứng của hình thang, bạn có thể sử dụng nó để lấy thông tin về các cạnh và tính chu vi.

Phân loại chu vi của một hình thang mà bạn nên biết

Chu vi của hình thang có thể được chia thành hai loại chính: chu vi bên ngoài và chu vi bên trong.

Chu vi ngoài

Chu vi ngoài của hình thang là tổng chiều dài tất cả các cạnh và các đoạn thẳng tạo nên hình thang, kể cả đáy và các cạnh. Đây là chu vi bên ngoài của hình thang, xác định toàn bộ đường viền của nó.

Chu vi bên trong

Chu vi bên trong của hình thang là tổng độ dài các cạnh bên của hình thang, không bao gồm cạnh đáy. Đây là chu vi bên trong một hình thang, chỉ tính cạnh của các cạnh bên chứ không tính cạnh của cạnh dưới.

Công thức tính chu vi của một hình thang

Để tính chu vi hình thang, ta có thể sử dụng công thức sau:

Chu vi = Cạnh thứ nhất của đáy + Cạnh thứ hai của đáy + Cạnh thứ nhất + Cạnh thứ hai

Hoặc có thể viết tắt công thức như sau:

Chu vi = a + b + c + d Trong đó:a và b là độ dài 2 cạnh đáy (đôi khi còn gọi là đáy dài và đáy ngắn).

c và d là độ dài hai cạnh. Công thức trên áp dụng cho các hình thang có các cạnh và các đoạn thẳng thẳng hàng và không cắt nhau. Nếu hình thang có các cạnh và đoạn thẳng không thẳng hàng hoặc không cắt nhau thì công thức tính chu vi có thể thay đổi tùy theo tính chất cụ thể của hình thang đó.

Chú ý rằng trong trường hợp đặc biệt hình thang là hình vuông hoặc hình chữ nhật thì công thức tính chu vi thay đổi tùy theo tính chất của hình vuông hoặc hình chữ nhật đó.

Ngoài ra, nếu biết góc và chiều cao của hình thang, bạn có thể sử dụng các công thức khác như định lý Pythagore để tính chu vi hình thang. Tuy nhiên, công thức trên là phương pháp đơn giản và phổ biến nhất để tính chu vi hình thang.

Cách giải một bài toán liên quan đến chu vi hình thang

Để giải bài toán về chu vi hình thang,các bạn làm theo các bước sau:

• Bước 1:Đọc và hiểu bài toán: Đầu tiên, hãy đọc kỹ bài toán để hiểu yêu cầu và thông tin về hình thang. Xác định các thông số như độ dài cạnh, đoạn thẳng hoặc góc của hình thang.
• Bước 2:Xác định công thức: Dựa vào thông tin đã cho và yêu cầu của bài toán hãy xác định công thức tính chu vi hình thang.Nói chung, công thức tính chu vi hình thang là tổng độ dài các cạnh và các đoạn thẳng tạo nên hình thang, như đã nêu ở câu hỏi trước.
• Bước 3:Gán giá trị cho tham số: Gán giá trị cho các biến tương ứng với các tham số đã biết trong bài toán. Chúng bao gồm độ dài của các cạnh, đoạn thẳng hoặc góc của hình thang.
• Bước 4:Tín và đưa ra kết quả: Áp dụng công thức tính chu vi hình thang đã xác định và tính chu vi bằng cách thay các giá trị đã gán trong công thức. Thực hiện tính toán để có được kết quả cuối cùng.
• Bước 5:Kiểm tra lại kết quả: Đảm bảo bạn tính đúng và kết quả phù hợp. Kiểm tra các bước tính toán và đảm bảo không xảy ra sai sót khi giải bài toán.
• Bước 6:Trình bày kết quả: Nêu kết quả cuối cùng theo yêu cầu của bài toán. Kết quả có thể làm tròn hoặc biểu thị dưới dạng phân số tùy theo yêu cầu của câu hỏi.

Cách tính các cạnh của chu vi một hình thang

Để tính các cạnh của chu vi hình thang, bạn cần biết đủ thông tin về hình thang, chẳng hạn như độ dài cạnh, góc hoặc đoạn thẳng liên quan. Tùy thuộc vào thông tin cụ thể có sẵn, bạn có thể sử dụng các phương pháp và công thức sau để tính các cạnh của chu vi hình thang:

Nếu bạn biết độ dài các cạnh

Nếu bạn đã biết độ dài các cạnh, chỉ cần cộng chúng lại với nhau.

Công thức tính là: Chu vi = Cạnh đáy thứ nhất + Cạnh đáy thứ hai + Cạnh cạnh thứ nhất + Cạnh cạnh thứ hai.

Nếu biết độ dài cạnh dưới và độ dài cạnh bên

Trong trường hợp này, bạn chỉ cần biết độ dài cạnh dưới và độ dài cạnh bên.

Công thức sẽ là: Chu vi = Đáy + Cạnh 1 + Cạnh 2.

Nếu bạn biết độ dài các cạnh và một góc

Nếu bạn biết độ dài các cạnh và một góc, bạn có thể sử dụng định luật cosin để tính độ dài từ các cạnh khác. Sau đó cộng các cạnh lại với nhau để tính chu vi.

Nếu biết độ dài các cạnh và chiều cao

Nếu biết thông tin về độ dài các cạnh và chiều cao thì có thể sử dụng công thức tính chu vi hình thang:

Chu vi = Đáy thứ nhất + Cạnh đáy thứ hai + Thứ nhất Cạnh bên + Cạnh bên thứ hai .

Biết đoạn thẳng chia thành các phần bằng nhau

Trong một số trường hợp, hình thang có các đoạn thẳng chia đường chéo thành các phần bằng nhau. Trong trường hợp này, bạn có thể tính các cạnh bằng phương pháp chia tỷ lệ.

Bài tập áp dụng

Bài tập 1:

Hình thang ABCD có đáy AB và CD là hai cạnh đối của hình thang. Đường cao AH của hình thang có độ dài 8 cm. Biết độ dài cạnh BC là 12 cm. Hãy tính chu vi của hình thang ABCD.

Đáp án :

Đường cao AH cắt đáy AB và CD thành hai đoạn thẳng bằng nhau. Vậy, độ dài đáy AB là 12 cm / 2 = 6 cm.

Chu vi của hình thang ABCD là: AB + BC + CD + DA = 6 cm + 12 cm + 6 cm + 8 cm = 32 cm.

Bài tập 2:

Hình thang ABCD có hai đáy AB và CD song song và bằng nhau. Cạnh BC của hình thang có độ dài 6 cm. Biết rằng đường cao của hình thang có độ dài 4 cm. Hãy tính chu vi của hình thang ABCD.

Đáp án :

Đường cao của hình thang cắt đáy AB và CD thành hai đoạn thẳng bằng nhau. Vậy, độ dài đáy AB và CD là (6 cm + 4 cm) = 10 cm.

Chu vi của hình thang ABCD là: AB + BC + CD + DA = 10 cm + 6 cm + 10 cm + 6 cm = 32 cm.

Bài tập 3:

Hình thang ABCD có đáy AB và CD là hai cạnh đối của hình thang. Cạnh BC của hình thang có độ dài 10 cm. Góc giữa đường cao và đáy AB là 60 độ. Hãy tính chu vi của hình thang ABCD.

Đáp án:

Biết góc giữa đường cao và đáy AB là 60 độ, ta có thể tính độ dài đáy AB bằng cách sử dụng định lý cosin:

AB = BC / cos(60°) = 10 cm / 0.5 = 20 cm

Chu vi của hình thang ABCD là: AB + BC + CD + DA = 20 cm + 10 cm + 20 cm + 10 cm = 60 cm.

Bài tập 4:

Hình thang ABCD có đáy AB và CD là hai cạnh đối của hình thang. Biết rằng độ dài đáy AB là 8 cm và độ dài cạnh BC là 10 cm. Hãy tính chu vi của hình thang ABCD nếu chu vi của nó là 36 cm.

Đáp án:

Chu vi của hình thang ABCD là: AB + BC + CD + DA = 8 cm + 10 cm + CD + DA = 36 cm.

Từ đó, ta suy ra CD + DA = 36 cm - 18 cm = 18 cm.

Vì AB và CD là hai cạnh đối của hình thang, nên CD = AB = 8 cm.

Thay vào biểu thức trên, ta có: 8 cm + DA = 18 cm.

Do đó, DA = 18 cm - 8 cm = 10 cm.

Vậy, chu vi của hình thang ABCD là: AB + BC + CD + DA = 8 cm + 10 cm + 8 cm + 10 cm = 36 cm.

Kết luận

Trên đây là một số bài tập tự luận và đáp án về cách tính chu vi của hình thang cân. Hy vọng rằng những bài tập này đã giúp bạn hiểu rõ hơn về cách tính toán chu vi của hình thang dựa trên các thông tin và công thức liên quan.