So sánh các số có nhiều phân số, định nghĩa và bài tập áp dụng

Cách so sánh các số có nhiều phân số được hiểu là tìm UCLN của các mẫu số hãy cùng chúng tôi tìm hiểu về cách so sánh cũng như bài tập áp dụng nhé.

So sánh các số và phân số là bài toán thường gặp của nhiều người, đặc biệt là với các bài toán phức tạp. Nhưng với những hàm cụ thể và logic thì việc so sánh sẽ không đơn giản. Trong bài viết này của thayphu, chúng ta sẽ tìm hiểu những bước cần thực hiện để so sánh các số có nhiều phân số

Giới thiệu về phân số và cách biểu diễn chúng

Giới thiệu về phân số và cách biểu diễn chúng

So sánh phân số là một phương pháp tính toán cho thấy cách chia một số thành các phần bằng nhau. Chúng được chia thành hai phần chính:

• Số lượng: Cho biết số lượng đơn vị được phân bổ.
• Thành phần: Cho biết số được chia thành bao nhiêu phần bằng nhau.

Phân số được biểu diễn dưới dạng a/b; trong đó a là số và b là đơn vị.

Ví dụ: 3/4 là phân số và số 3 là số 4 là đơn vị

Phân số cũng có thể được biểu diễn dưới dạng số nguyên nếu số đó lớn hơn số đó. Ví dụ: 5 3/4 là một số hỗn hợp trong đó 5 là số nguyên và 3/4 là một nửa số.

Các bước cơ bản để so sánh các số có nhiều phân số

Để so sánh các số có nhiều phân số ta cần nắm vững các quy tắc. Dưới đây chúng tôi đã tổng hợp những quy tắc giúp bạn dễ dàng trong việc phân tích các phân số

Bước 1: Tìm ước chung (UCLN) của phân số

Việc tìm UCLN của phân số sẽ giúp chúng ta quy đổi tất cả các phân số khác nhau về cùng một phân số.

Điều này làm cho việc so sánh dễ dàng hơn.

Bước 2: Biến các phần thành các phần riêng biệt

Sau khi tìm được UCLN, chia tổng từng phần cho UCLN để ghép các phần mới lại với nhau.

Số của mỗi phần được chia cho các phần tương ứng và nhân lên.

Bước 3: So sánh trực tiếp bằng cách đếm

Chỉ so sánh bằng cách đếm nếu tất cả các phần có cùng số với nhau.

Phân số có số lớn nhất sẽ là phân số lớn nhất.

Bước 4: Giải hỗn số

Khi so sánh các hỗn số, trước tiên hãy chuyển chúng thành phân số bằng nhau.

Sau khi đã chuyển về phân số ta tiến hành để so sánh.

Bước 5: Chú ý đặc biệt

Khi so sánh các số có nhiều phân số âm ta cần chú ý đến dấu trừ trong số.

Bất kỳ phân số nào trong số có dấu âm sẽ nhỏ hơn phân số không có dấu âm.

Ví dụ:

Cho các phân số: 1/2, 3/4, 5/6

• Bước 1: Tìm UCLN của 2, 4, 6 là 2
• Bước 2: Chuyển các phân số về cùng mẫu số 2:

1/2 = 3/4 = 5/6 = 6/12

Sau khi đặt các phân số cùng mẫu số, chúng ta có thể dễ dàng so sánh chúng bằng cách so sánh trực tiếp các tử số:

6/12 < 9/12 < 10/12

Một số dạng bài toán về cách so sánh các số có nhiều phân số

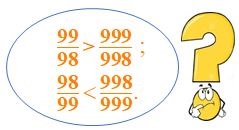
Một số dạng bài toán về cách so sánh các số có nhiều phân số

Dưới đây chúng tôi đã tổng hợp những dạng toán mà thường xuyên gặp về các so sánh các số

Dạng 1: Chuyển số hỗn hợp thành phân số thuần túy

Hướng dẫn: Lấy phần nguyên nhân với mẫu số, rồi cộng với phần phân số.

Ví dụ: Chuyển 3 1/4 thành phân số đơn giản

Giải: 3 1/4 = (3 * 4 + 1) / 4 = 13/4

Đáp án: 13/4

Dạng 2: Tìm ước chung lớn nhất (UCLN) của các mẫu số

Hướng dẫn: Sử dụng thuật toán Euclid để tìm UCLN.

Ví dụ: Tìm UCLN của 12, 18, 24.

Giải: UCLN(12, 18, 24) = 6

Đáp án: 6

Dạng 3: Chuyển về cùng mẫu số

Hướng dẫn: Nhân tử số và mẫu số của mỗi phân số với UCLN các mẫu số.

Ví dụ: Chuyển 2/3, 3/5, 5/7 về cùng mẫu số.

Giải: UCLN(3, 5, 7) = 1, nên 2/3 = 14/21, 3/5 = 12/21, 5/7 = 15/21

Đáp án: 14/21, 12/21, 15/21

Dạng 4: So sánh trực tiếp các tử số

Hướng dẫn: So sánh trực tiếp các tử số khi các phân số có cùng mẫu số.

Ví dụ: So sánh 14/21, 12/21, 15/21.

Giải: 15/21 > 14/21 > 12/21

Đáp án: 15/21 > 14/21 > 12/21

Một số lưu ý khi so sánh các số có nhiều phân số

Dưới đây là những lưu ý mà bạn cần nắm rõ khi so sánh các số

Chuyển đổi các số về cùng một dạng

Điều quan trọng là phải chuyển đổi tất cả các phần về cùng một giá trị trước khi so sánh. Điều này giúp chúng ta có được cơ sở tốt để so sánh.

Khi chuyển sang các số có cùng một phân số ta lập tử số và tổng của từng phân số UCLN trong mẫu số.

Nhìn vào từng phần của phân số

Khi so sánh các số, hãy nhìn vào từng phần để dễ dàng so sánh chứ không được nhìn các phần quan trọng

Kiểm tra UCLN

Tìm UCLN của mẫu số là bước quan trọng trước khi quay về số cũ.

Nếu UCLN là 1 thì giá trị đã là một.

So sánh các số

Nếu các phân số giống nhau ta sẽ so sánh trực tiếp các số.

Cách kết hợp

Các bước như thay đổi một giá trị, so sánh các số, xét phép cộng phải kết hợp mới có kết quả đúng.

Bài tập áp dụng

Câu 1: Số nào lớn hơn: 3/5 hay 4/7?

A) ⅗

B) 4/7

Đáp án: A) 3/5

Câu 2: So sánh 2 5/8 và 2 3/4.

A) 2 5/8 < 2 3/4

B) 2 5/8 > 2 3/4

C) 2 5/8 = 2 ¾

Đáp án: A) 2 5/8 < 2 3/4

Câu 3: Số nào lớn hơn: 5 2/3 hay 5 3/5?

A) 5 ⅔

B) 5 ⅗

C) Bằng nhau

Đáp án: B) 5 3/5

Câu 4: So sánh 7/8 và 15/16.

A) 7/8 < 15/16

B) 7/8 > 15/16

C) 7/8 = 15/16

Đáp án: A) 7/8 < 15/16

Câu 5: Số nào lớn hơn: 4 1/2 hay 4 3/7?

A) 4 ½

B) 4 3/7

C) Bằng nhau

Đáp án: A) 4 1/2

Câu 6: So sánh 2 1/4 và 2 3/8.

A) 2 1/4 < 2 3/8

B) 2 1/4 > 2 3/8

C) 2 1/4 = 2 3/8

Đáp án: B) 2 1/4 > 2 3/8

Câu 7: Số nào lớn hơn: 6 5/6 hay 7 1/12?

A) 6 5/6

B) 7 1/12

C) Bằng nhau

Đáp án: B) 7 1/12

Câu 8: So sánh 3 1/3 và 3 2/5.

A) 3 1/3 < 3 2/5

B) 3 1/3 > 3 ⅖

C) 3 1/3 = 3 2/5

Đáp án: B) 3 1/3 > 3 2/5

Câu 9: Số nào lớn hơn: 5 1/4 hay 5 3/8?

A) 5 ¼

B) 5 ⅜

C) Bằng nhau

Đáp án: B) 5 3/8

Câu 10: So sánh 8 2/7 và 8 3/5.

A) 8 2/7 < 8 3/5

B) 8 2/7 > 8 3/5

C) 8 2/7 = 8 3/5

Đáp án: B) 8 2/7 > 8 3/5

Trên đây là một số lý thuyết cũng như bài tập về cách so sánh các số có nhiều phân số trong chương trình toán lớp 4, nếu bạn có thắc mắc gì thì liên hệ với thayphu.net nhé