Bất đẳng thức Minkowski, tổng hợp lý thuyết và bài tập

Bất đẳng thức Minkowski có dạng như thế nào? Cách ứng dụng để giải bài tập nhanh chóng, đơn giản giúp các em hoàn thành hiệu quả nhất.

Bất đẳng thức là chuyên đề khá khó nhằn trong chương trình Toán phổ thông với nhiều dạng bài phức tạp. Vì vậy đòi hỏi các em cần có khả năng vận dụng công thức một cách hợp lý. Và bất đẳng thức Minkowski chính là trợ thủ giúp giải các phương trình, bất phương trình chứa căn hay chứng minh bất đẳng thức.

Bài viết sau đây của thayphu sẽ cập nhật chi tiết về lý thuyết và các bài tập vận dụng.

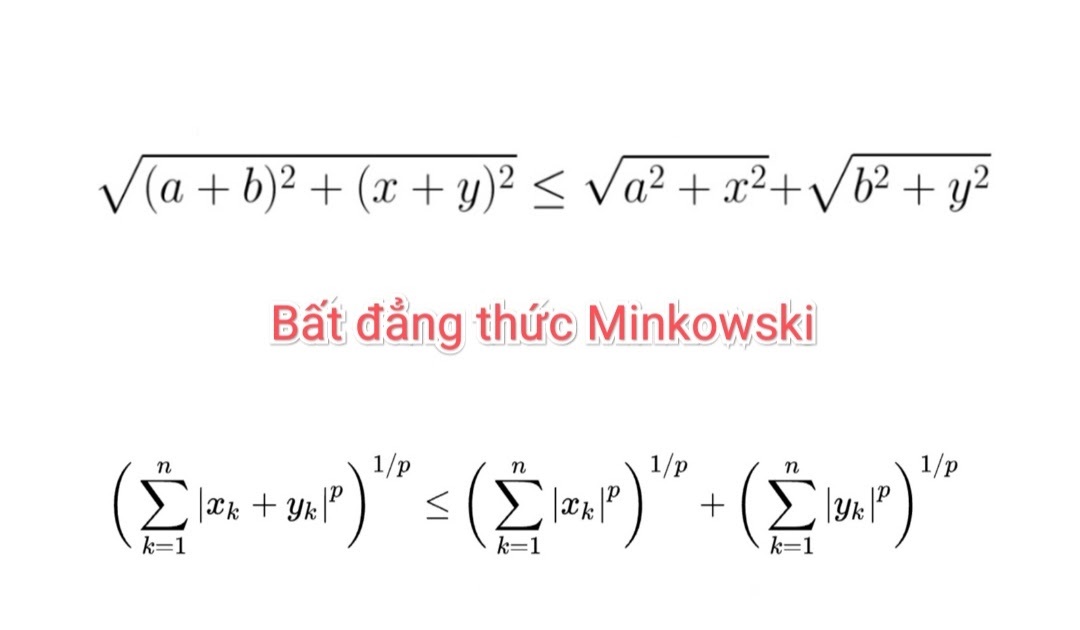
Tìm hiểu chi tiết về bất đẳng thức Minkowski

Lý thuyết về bất đẳng thức Minkowski

Dạng tổng quát

Cho 2 dãy số thực là a1, a2,..., an và b1, b2,..., bn, ta sẽ được:

a21 + b2 1 + a22 + b2 2 + … + a2n + b2 n >= (a1 + a2 + ... + an)2 + (b1 + b2 + ... +bn)2

Dấu bằng sẽ xảy ra khi: a1 / b1 = a2 / b2 = … = an / bn

Quy ước: Nếu b1 = 0 thì a1 = 0 và tương tự với b2, b3,..., bn cũng vậy.

Dạng cụ thể

• Dạng 1: Ta cho a,b,c,d thuộc R, khi đó:

a2+ b2 + c2 + d2 >= (a+c)2+ (b+d)2

Dấu bằng chỉ xảy ra khi: a/b = c/d

Dạng 2: Cho a,b,c,d,e,f thuộc R, ta có:

a2+ b2 + c2 + d2 + e2 + f2 >= (a+ c+ e)2+ (b+d+f)2

Dấu bằng chỉ xảy ra khi: a/b = c/d = e/f

Chứng minh bất đẳng thức Minkowski

Với mọi a, b, x, y thuộc R hãy chứng minh rằng ta luôn có bất đẳng thức sau:

a2+ x2 + b2+ y2 >= (a+b)2+ (x + y)2

Cách giải:

Ta tiến hành bình phương 2 vế và biến đổi tương đương:

a2+ x2 + b2+ y2 >= (a+b)2+ (x + y)2

⇔ a^2 + x^2 + b^2 + y^2 + 2(a2 + x2) (b2+ y2) >= a^2 + x^2 + b^2 + y^2 +2ab + 2x

⇔ 2(a2+x2) (b2+y2) >= 2ab + 2xy

⇔ (a2+ x2) (b2+ y2) >= ab + xy (1)

Trường hợp nếu ab + xy <= 0 thì (1) luôn đúng

Trường hợp nếu ab + xy > 0 thì (1)

⇔ (a^2 + x^2) (b^2 + y^2) >= (ab + xy)^2 ⇔ (bx - ay)^2 luôn đúng.

Như vậy dấu = của đẳng thức sẽ xảy ra khi bx = ay.

Lưu ý: Ta cũng có thể chứng minh bất đẳng thức trên bằng cách sử dụng bất đẳng thức vecto dưới đây:

Đặt vecto u = (a;x) và vecto v = (b;y)

Khi đó vecto u + vecto v = (a+b; x+y)

Từ bất đẳng thức vecto |vecto u + vecto v| <= |vecto u| + |vecto v| và công thức độ dài vecto sẽ ra điều cần phải chứng minh.

Nếu áp dụng 2 lần bất đẳng thức đã cho ở trên ta có bất đẳng thức Minkowski như sau:

a2 + x2 + b2 + y2 + c2 + z2 >= (a + b+ c)2+ (x+y+z)2với a, b, c, x, y, z đều thuộc R.

Áp dụng bất đẳng thức để giải các dạng bài tập

Các dạng bài tập ứng dụng bất đẳng thức Minkowski

Dạng 1 - Giải bài tập bất phương trình

Cho a, b, c > 0 và ab + bc + ca = abc

Ta dùng bất đẳng chứng Minkowski để chứng minh:

b2 + 2a2 / ab + c2 + 2b2/ bc + a2 + 2c2 / ca >= 3

Cách giải:

Thực hiện biến đổi giả thiết:

ab + bc + ca = abc ⇔ 1/a + 1/b + 1/c = 1

Ta có: b2+ 2a2 / ab + c2 + 2b2 / bc + a2 + 2c2 / ca

= 1/a2+ 2/b2 + 1/b2+ 2/c2 + 1/c2+ 2/a2

Ứng dụng bất đẳng thức Minkowski ta có:

1/a2+ (2/b)2 + 1/b2+ (2/c)2 + 1/c2+ (2/a)2 >= (1/a + 1/b + 1/c)2+ 2(1/a + 1/b + 1/c)2

Với 1/a + 1/b + 1/c = 1

=> b2 + 2a2 / ab + c2 + 2b2 / bc + a2 + 2c2 / ac >= 3

Các dạng bài tập chi tiết và lời giải

Dạng 2 - Giải bài tập về số phức

Ví dụ cho số phức z = a + bi (với a, b thuộc R) thỏa mãn |z - 4 - 3i| = |z - 2 + 1|

Yêu cầu hãy tính giá trị biểu thức:

P = a^2 + b^2 khi |z + 1 - 3i| + |z - 1 + i| đạt giá trị nhỏ nhất.

Cách giải:

Từ giả thiết ta sẽ có:

(a - 4)^2 + (b - 3)^2 = (a - 2)^2 + (1 - b)^2 ⇔ b = 5 - a

|z + 1 - 3i| + |z - 1 + i| = (a + 1)2+ (b-3)2 + (a-1)2+ (b + 1)2

= (a + 1)2 + (2-a)2 + (a - 1)2 + (6-a)2

= 2a2-2a + 5 + 2a2-14a + 37

= (1/2 - 2 a)2+ (9/2 )2 + (2 a- 7/2 )2+ (25/2 )2

= (1/2 - 2 a+2 a -7/2 )2+ (9/2 +25/2 )2 = 52

Dấu bằng sẽ xảy ra khi:

((1/2 - 2 a) / (2 a - 7/2 = 9/2 / 25/2

⇔ a = 13/8 và b = 27/8

=> P = (13^2 + 27^2) / 8^2 = 449/32

Dạng 3 - Giải bài tập hình học tọa độ

Trong không gian Oxyz cho mặt cầu (S): (x-1)^2 + (y - 1)^2 + z^2 = 25 cùng 2 điểm là A (7;9;0) và B (0;8;0). Với M là điểm di động trên mặt cầu (S). Hãy tính giá trị nhỏ nhất của biểu thức MA + 2MB.

Cách giải:

M(x;y;z) thuộc (S) => (x - 1)^2 + (y - 1)^2 + z^2 = 25

Như vậy ta có:

MA + 2MB = (x -7)2 + (y - 9)2 + z2 + 2x2+ (y-8)2 +z2

= (x -7)2 + (y - 9)2 + z3 + 3[(x -1)2+ (y - 1)2+z2-25] + 2x3(y -8)2+z2

= 2[(5/2 - x)2+ (3 - y)2+ (-z)2 + x2+ (y-8)2 +z2]

>= 2[(5/2 - x +x)2+ (3 - y+ 8 - y)2+ (-z +z)2

Dấu = sẽ xảy ra khi:

(5/2 -x) / x = (3-y) / (y - 8) = k > 0

z = 0

(x - 1)^2 + (y - 1)^2 + z^2 = 25

⇔ x = 1; y = 6 và z = 0

Kết luận M (1;6;0)

Bài viết vừa tổng hợp đầy đủ về lý thuyết, công thức của bất đẳng thức Minkowski và cách ứng dụng vào các dạng bài tập. Hy vọng các em đã có những giây phút học tập hiệu quả và hoàn thành tốt các bài tập!