Phương trình bậc hai 4x ^ 2 - 5x - 12 là gì và cho ví dụ minh họa

Phương trình bậc hai có dạng 4x ^ 2 - 5x - 12 = 0 trong đó 4, 2 và 5 là các hệ số đã biết và x là ẩn cần tìm.Định nghĩa,tính chất ,ví dụ minh họa.

Trong toán học, giải phương trình là một quá trình quan trọng giúp chúng ta tìm giá trị của các biến trong phương trình. Một phương trình cụ thể mà chúng ta sẽ học là phương trình bậc hai, cụ thể hơn là chúng ta sẽ xét phương trình 4x^2 - 5x - 12 = 0. Trong bài viết này của thayphu sẽ cùng nhau tìm hiểu cách giải phương trình này.

Định nghĩa về phương trình 4x ^ 2 - 5x - 12

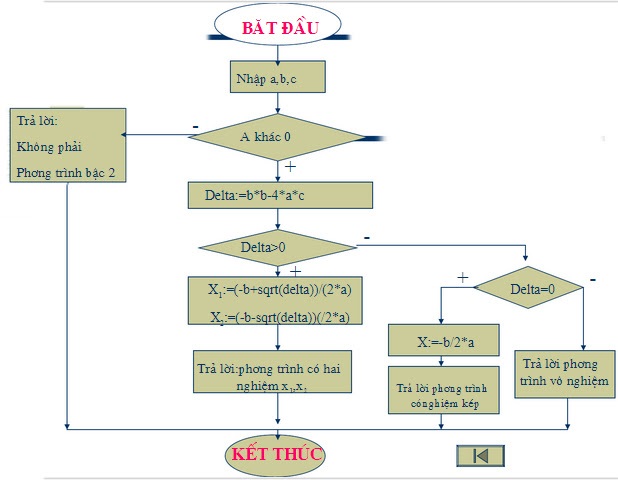
Định nghĩa về phương trình 4x ^ 2 - 5x - 12

Phương trình 4x^2 - 5x - 12 là phương trình bậc hai, trong đó x là biến và các hệ số của phương trình đã cho là 4, -5 và -12.Phương trình này được viết dưới dạng tổng lũy thừa của biến x, tức là x^2 và x, cùng với các hệ số tương ứng.

Trong trường hợp này, hệ số x^2 là 4, hệ số x là -5 và hệ số tự do là -12.

Mục tiêu của chúng ta là tìm giá trị của biến x để phương trình trở thành mệnh đề đúng. Điều này có nghĩa là chúng ta tìm x sao cho khi thay giá trị này vào phương trình thì chúng ta nhận được kết quả 0.

Nguồn gốc của phương trình 4x ^ 2 - 5x - 12 ở đâu?

Phương trình 4x^2 - 5x - 12 không có nguồn gốc cụ thể. Nó là một phương trình bậc hai thông thường được tạo ra bằng cách thay thế các hệ số vào phương trình. Phương trình này có thể được xây dựng theo nhiều cách khác nhau và có thể xuất hiện trong nhiều bài toán khác nhau trong toán học và các lĩnh vực liên quan.

Một phương trình bậc hai như trên có thể được tạo ra bằng cách áp dụng nhiều phép biến đổi và toán học khác nhau, hoặc nó có thể là một phần của một bài toán cụ thể đòi hỏi phải giải phương trình.

Vậy phương trình 4x^2 - 5x - 12 không có gốc cụ thể.Nó chỉ là một phương trình bậc hai thông thường mà chúng ta có thể giải bằng các phương pháp thông thường của đại số.

Điểm nổi bật của phương trình 4x ^ 2 - 5x - 12

Phương trình 4x^2 - 5x - 12 có các tính chất nổi bật sau: Bậc mũ của phương trình:

• Phương trình này là phương trình bậc hai, số mũ cao nhất của biến x^2. Điều này có nghĩa là phương trình trong hầu hết các trường hợp có thể có hai nghiệm.
• Hệ số: Trong phương trình này, hệ số x^2 là 4, hệ số x là -5 và hệ số tự do là -12.Các hệ số này xác định hình dạng và vị trí của đồ thị của phương trình.
• Dạng phương trình: Phương trình được viết dưới dạng tổng lũy thừa của x, từ lớn nhất đến nhỏ nhất. Đây là dạng chuẩn của phương trình bậc hai.
• Lời giải: Phương trình có thể có hai nghiệm, một nghiệm hoặc không có nghiệm tùy thuộc vào giá trị Delta (biểu thức dưới dấu căn bậc hai trong công thức nghiệm).
• Đồ thị:Đồ thị của phương trình này là một đường cong parabol có thể mở lên hoặc mở xuống tùy theo giá trị của hệ số a. Sơ đồ có thể được vẽ để hiển thị biểu diễn hình học của phương trình.

Những điểm nổi bật này giúp chúng ta có cái nhìn tổng quan về phương trình 4x^2 - 5x - 12 và làm cơ sở cho những nghiên cứu tiếp theo và giải phương trình này.

Một số dạng toán về phương trình 4x^2 - 5x - 12

Dưới đây là một số dạng toán liên quan đến phương trình 4x^2 - 5x - 12:

Giải phương trình

Tìm các giá trị của x sao cho phương trình 4x^2 - 5x - 12 = 0 trở thành một câu đúng Để giải phương trình này, có thể sử dụng công thức Bhaskara hoặc các phương pháp khác như hoàn thành khối lập phương.

Xác định đồ thị

Vẽ đồ thị của phương trình 4x^2 - 5x - 12 trong hệ tọa độ.Đồ thị là một đường cong parabol và có thể được sử dụng để xác định các tính chất hình học của phương trình.

Tìm điểm cực trị

Xác định giá trị nhỏ nhất hoặc lớn nhất của hàm số 4x^2 - 5x - 12. Điểm cực trị ứng với điểm trên đồ thị mà tại đó hàm số đạt giá trị cực tiểu hoặc cực đại.

Tìm khoảng giá trị

Xác định các khoảng giá trị của x mà phương trình 4x^2 - 5x - 12 thỏa mãn một điều kiện nào đó, ví dụ x > 0 hoặc x thuộc khoảng [-1, 2]. Để làm điều này, chúng ta có thể xem xét sự biến thiên của hàm số trong những khoảng thời gian nhất định.

Tính chất đặc biệt

Xét tính chất đặc biệt của phương trình 4x^2 - 5x - 12. Ví dụ: phương trình có nghiệm nguyên hay không, có nghiệm kép hay không, có nghiệm phức hay không, và cách tìm giá trị Delta để xác định số nghiệm.

Bài toán ứng dụng

Áp dụng phương trình 4x^2 - 5x - 12 vào các bài toán thực tế như tính diện tích, thể tích, vận tốc theo thời gian. Bằng cách giải phương trình này, chúng ta có thể tìm thấy các giá trị của biến x liên quan đến bài toán cụ thể.

Ưu điểm khi giải phương trình 4x^2 - 5x - 12

Một số ưu điểm đáng chú ý khi giải phương trình 4x^2 - 5x - 12 = 0:

• Áp dụng công thức nghiệm: Phương trình 4x^2 - 5x - 12 = 0 là phương trình bậc hai có công thức nghiệm đã được biết rõ. Bằng cách áp dụng công thức Bhaskara chúng ta có thể tính toán chính xác các giá trị của x dựa trên các hệ số đã cho.
• Độ chính xác: Sử dụng công thức nghiệm ta có thể tìm được giá trị chính xác của x.Điều này giúp chúng ta tự tin vào kết quả và đáp ứng được nhu cầu của bài toán.
• Phạm vi ứng dụng rộng rãi: Phương trình 4x^2 - 5x - 12 là phương trình bậc hai thông dụng và có thể sử dụng trong nhiều lĩnh vực toán học, khoa học, công nghệ khác nhau. Giải phương trình này giúp ta tìm được giá trị của biến x trong bài toán thực tế.
• Phương pháp tính toán linh hoạt: Ngoài công thức Bhaskara, còn có rất nhiều phương pháp giải phương trình bậc hai khác. Điều này cho phép chúng ta sử dụng các phương pháp khác nhau tùy thuộc vào loại phương trình và tình huống cụ thể.
• Hiểu tính chất của đồ thị: Phương trình 4x^2 - 5x - 12 = 0 có đồ thị parabol. Bằng cách giải phương trình này, chúng ta có thể hiểu rõ hơn về hình dạng và tính chất của đồ thị parabol, chẳng hạn như tọa độ các điểm góc, trục đối xứng và điểm cực trị.

Những lưu ý khi giải phương trình 4x^2 - 5x - 12

Khi giải phương trình 4x^2 - 5x - 12 = 0, đây là một số gợi ý quan trọng:

• Kiểm tra tính đúng đắn của phương trình: Đảm bảo phương trình được viết đúng và tất cả các số hạng được sắp xếp theo thứ tự giảm dần. Sắp xếp lại phương trình nếu cần thiết để đảm bảo tính chính xác của các hệ số.
• Tìm giá trị Delta: Delta (Δ) trong phương trình bậc hai được tính bằng Δ = b^2 - 4ac, trong đó a, b và c lần lượt là các hệ số của x^2, x và số hạng tự do .Tính toán delta rất quan trọng để xác định số lượng và loại giải pháp.
• Xác định số nghiệm: Dựa vào giá trị Delta ta xác định được số nghiệm của phương trình. Nếu Delta > 0 thì phương trình có hai nghiệm khác nhau; nếu Delta = 0 thì phương trình có nghiệm kép; Nếu Delta 0 thì có thể sử dụng công thức Bhaskara để tính nghiệm của phương trình. Công thức này bao gồm hai nghiệm riêng biệt: x = (-b + √Δ) / (2a) và x = (-b - √Δ) / (2a).
• Rút gọn kết quả: Sau khi tính toán, rút gọn kết quả nếu có thể. Điều này giúp đơn giản hóa các giá trị và làm cho kết quả dễ đọc và dễ hiểu hơn.
• Kiểm tra lại: Sau khi tìm được kết quả, kiểm tra lại bằng cách thay giá trị x vào phương trình ban đầu.Nếu cả hai vế của phương trình đều bằng nhau thì kết quả là đúng.

Bài tập áp dụng

Bài tập 1: Giải phương trình 4x^2 - 5x - 12 = 0 bằng cách sử dụng công thức Bhaskara.

Đáp án:

Ta có phương trình 4x^2 - 5x - 12 = 0.

Áp dụng công thức Bhaskara:

Δ = b^2 - 4ac

= (-5)^2 - 4(4)(-12)

= 25 + 192 = 217.

√Δ = √217.

x₁ = (-(-5) + √217) / (2(4))

= (5 + √217) / 8.

x₂ = (-(-5) - √217) / (2(4))

= (5 - √217) / 8.

Bài tập 2: Tìm các giá trị của x để phương trình 4x^2 - 5x - 12 = 0 có nghiệm kép.

Đáp án:

Phương trình có nghiệm kép khi Δ = 0.

Δ = b^2 - 4ac

= (-5)^2 - 4(4)(-12)

= 25 + 192 = 217.

217 = 0.

Vì Δ ≠ 0, nên phương trình không có nghiệm kép.

Bài tập 3: Vẽ đồ thị của hàm số y = 4x^2 - 5x - 12.

Đáp án:

Đồ thị của hàm số y = 4x^2 - 5x - 12 là một đường cong parabol. Từ các thông tin đã cho, ta có thể xác định tọa độ của đỉnh, đường đối xứng và điểm cực trị.

Bài tập 4: Xác định khoảng giá trị của x mà phương trình 4x^2 - 5x - 12 = 0 thỏa mãn x > 0.

Đáp án:

Để xác định khoảng giá trị của x, ta cần giải phương trình và xem xét các giá trị x thỏa mãn điều kiện x > 0.

Giải phương trình 4x^2 - 5x - 12 = 0 và xác định các nghiệm. Sau đó, xem xét từng nghiệm để kiểm tra xem liệu nó thỏa mãn điều kiện x > 0 hay không.

Bài tập 5: Tìm giá trị nhỏ nhất của hàm số y = 4x^2 - 5x - 12.

Đáp án: Để tìm giá trị nhỏ nhất của hàm số, ta cần xác định điểm cực trị. Điểm cực trị tương ứng với điểm trên đồ thị mà hàm số đạt giá trị nhỏ nhất.

Bài tập 6: Xác định các giá trị của delta (Δ) để phương trình 4x^2 - 5x - 12 = 0 có hai nghiệm phân biệt.

Đáp án: Phương trình có hai nghiệm phân biệt khi Δ > 0. Để xác định các giá trị của delta, ta tính Δ = b^2 - 4ac và tìm các giá trị của Δ mà thỏa mãn Δ > 0.

Bài tập 7: Áp dụng phương trình 4x^2 - 5x - 12 vào một bài toán ứng dụng cụ thể, ví dụ như tính diện tích hoặc thể tích.

Đáp án: Dựa vào bài toán ứng dụng cụ thể, ta có thể sử dụng phương trình 4x^2 - 5x - 12 để tính diện tích hoặc thể tích của một hình học cụ thể. Ví dụ, nếu đề bài yêu cầu tính diện tích hình vuông có cạnh là x, ta có thể sử dụng phương trình để tìm giá trị x và sau đó tính diện tích.

Bài tập 8: Giải phương trình 4x^2 - 5x - 12 = 0 bằng phương pháp khác, chẳng hạn như phân tích thành nhân tử.

Đáp án: Để giải phương trình bằng phương pháp phân tích thành nhân tử, ta cần tìm các thừa số của phương trình và chia nó thành dạng nhân tử của các biểu thức nhỏ hơn. Sau đó, ta có thể tìm các giá trị của x bằng cách đặt mỗi nhân tử bằng 0 và giải các phương trình tương ứng.

Kết luận

Trên đây là những thông tin về phương trình 4x^2 - 5x - 12 = 0, cùng với các bài tập tương ứng. Hy vọng rằng những thông tin này đã giúp bạn làm quen với việc giải phương trình bậc hai và áp dụng các phương pháp khác nhau để tìm nghiệm.