Cách tìm số bị trừ và các dạng bài tập vận dụng cực hay

Số bị trừ là gì? Làm thế nào để tính số bị trừ? Kiến thức chung, tính chất và phương pháp tìm số bị trừ. Các bài tập vận dụng chi tiết của phép trừ.

Khi bắt đầu tiếp xúc với môn toán ở tiểu học, ngoài kiến thức về cách đếm những con số, các bạn học sinh còn được học về các phép tính. Trong đó, các kiến thức về phép tính trừ, số bị trừ, số trừ và hiệu là những kiến thức nền tảng quan trọng ở tiểu học. Vì vậy, trong bài viết này hãy cùng thayphu tìm hiểu về các kiến thức thú vị này là áp dụng chúng vào các dạng toán khác nhau nhé.

Kiến thức số bị trừ và số trừ cần nắm

Số bị trừ là gì?

Số bị trừ là số được trừ đi trong một phép tính trừ. Trong phép tính trừ, chúng ta có ba thành phần chính: số trừ, số bị trừ và kết quả (hay còn gọi là hiệu).

Nói cách khác, số bị trừ là số lượng ban đầu, còn số trừ là số lượng cần phải lấy ra. Kết quả của phép tính trừ là hiệu, là số lượng còn lại sau khi đã lấy đi số trừ.

Số trừ là gì?

Số trừ đại diện cho một số lượng hay giá trị mà chúng ta muốn loại bỏ hoặc giảm đi từ một số gốc (hay số bị trừ). Nó là số mà chúng ta trừ đi từ số bị trừ để tính ra kết quả.

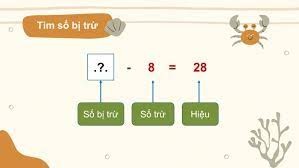
Ví dụ: 12 - 5 = 7

Trong đó: 12 là số bị trừ, 5 là số trừ và 7 là hiệu của phép tính trừ đó.

Tính chất của phép trừ

Phép trừ là một trong các phép tính cơ bản trong toán học, và nó có một số tính chất quan trọng. Dưới đây là một số tính chất của phép trừ:

• Tính chất giao hoán: Phép trừ không thỏa mãn tính chất giao hoán, có nghĩa là việc thay đổi vị trí của các số trong phép tính trừ sẽ dẫn đến kết quả khác nhau. Ví dụ: 5 - 3 không bằng 3 - 5.
• Tính chất kết hợp: Phép trừ có tính chất kết hợp, có nghĩa là kết quả của các phép trừ liên tiếp không phụ thuộc vào cách nhóm các số hạng. Ví dụ: (10 - 5) - 3 = 10 - (5 + 3) = 2.
• Tính chất phân phối: Phép trừ thỏa mãn tính chất phân phối với phép cộng. Điều này có nghĩa là a - (b + c) = (a - b) + (a - c). Ví dụ: 10 - (4 + 2) = (10 - 4) + (10 - 2) = 8 + 8 = 16.
• Phần tử đơn vị: Số 0 được gọi là phần tử đơn vị của phép trừ. Khi trừ một số cho chính nó, kết quả sẽ luôn là 0. Ví dụ: 7 - 7 = 0.
• Tính chất đối: Phép trừ có tính chất đối, có nghĩa là a - b = -(b - a). Điều này cho phép ta thay đổi vị trí của các số trong phép trừ mà không làm thay đổi kết quả. Ví dụ: 8 - 3 = -(3 - 8) = 5.

Cách tìm số bị trừ trong toán học

Phương pháp: Muốn tính một số bị trừ chưa biết, ta lấy số trừ cộng với hiệu. Kết quả của phép tính cộng này chính là số bị trừ.

Ví dụ: x - 7 = 4

Áp dụng phương pháp đã nêu ở trên, ta có:

x - 7 = 4

⇔ x = 4 + 7

⇔ x = 11

Vậy số bị trừ của phép tính này là x = 11.

Các dạng toán về số bị trừ và bài tập vận dụng

Dạng 1: Hoàn thành bảng

Bài tập 1: Điền các số còn thiếu vào bảng sau:

Gợi ý lời giải:

Ta có:

45 - 27 = 18

13 + 7 = 20

33 - 9 = 24

Vậy ta có thể hoàn thành bảng như sau:

Bài tập 2: Điền vào bảng (Bài 4/ 77, toán lớp 3 - tập 2, SGK Cánh Diều)

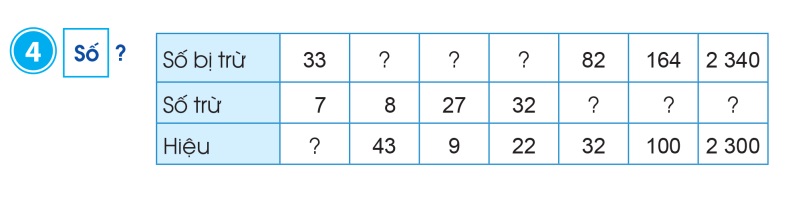
Gợi ý lời giải:

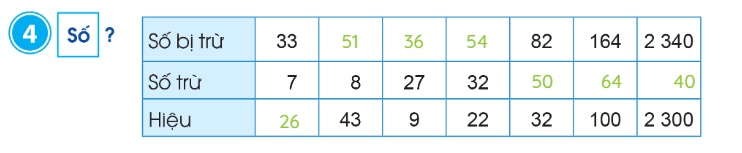
Dạng 2: Tìm x

Bài tập:Tìm x theo các phép toán dưới đây:

1. x - 2 = 9

2. 11 - x = 8

3. 23 - x = 12

4. x - 7 = 14

Gợi ý lời giải:

1. x - 2 = 9

x = 9 + 2

x = 11

2. 11 - x = 8

x = 11 - 8

x = 3

3. 23 - x = 12

x = 23 - 12

x = 11

4. x - 7 = 14

x = 14 + 7

x = 21

Dạng 3: Toán đố

Bài tập 1: Trong cửa hàng có 40 quyển sách, sau khi ông chủ bán đi một số quyển sách thì trong cửa hàng còn lại 13 quyển sách. Hỏi cửa hàng đã bán được bao nhiêu quyển sách ?

Gợi ý lời giải:

Cửa hàng đã bán được số quyển vở là:

40 - 13 = 27 (quyển sách)

Đáp số: 27 quyển sách.

Bài tập 2: Trong vườn của bà có 1 cây táo rất to và có nhiều quả táo. Bạn Bi đã hái 9 quả táo. Sau khi đếm lại số táo trên cây thì thấy còn 23 quả táo. Vậy lúc ban đầu trên cây có bao nhiêu quả táo?

Gợi ý lời giải:

Số táo ban đầu có trên cây là:

9 + 23 = 32 (quả táo)

Đáp số: 32 quả táo.

Kết luận

Trong môn toán, đặc biệt là chương trình toán tiểu học, số bị trừ đóng vai trò quan trọng trong phép tính trừ.Vì vậy, việc hiểu và thực hành tính toán số bị trừ sẽ giúp chúng ta nắm vững những kiến thức nền tảng toán học cơ bản. Bằng cách áp dụng phép trừ, chúng ta có thể tính toán số bị trừ một cách chính xác. Thế nên các bạn học sinh hay luyện tập các dạng toán về phép trừ, số bị trừ thật nhiều để nắm rõ và dễ dàng giải các dạng toán nâng cao hơn nữa nhé.