Cách tìm số hạng chưa biết và các dạng bài tập vận dụng

Khái niệm, tính chất và phương pháp tìm số hạng chưa biết trong phép tính cộng. Các dạng bài tập thú vị để vận dụng và ôn tập các số hạng.

Số hạng chưa biết trong toán học là một thành phần của biểu thức hoặc phép toán mà giá trị chính xác của nó chưa được xác định. Thay vì sử dụng một giá trị cố định, số hạng chưa biết được biểu diễn bằng một ký hiệu đại diện cho một giá trị chưa biết hoặc chưa được xác định trong bài toán. Đây được coi là một trọng những kiến thức quan trọng trong chương trình toán lớp 2, là nền tảng giúp các bạn giải các dạng toán nâng cao ở THCS.

Vì vậy, trong bài viết này, thayphu sẽ cùng các bạn học sinh tìm hiểu về số hạng chưa biết, cũng như làm các bài tập vận dụng cũng dạng toán này nhé.

Số hạng và số hạng chưa biết là gì?

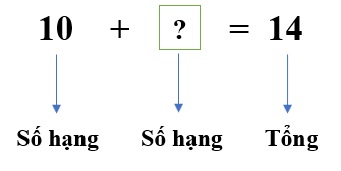
Ta có thể hiểu đơn giản số hạng là một thành phần của một tổng hay một phép tính cộng. Trong phép cộng, các số hạng được cộng với nhau để tạo thành một tổng.

Ví dụ: 5 + 3 = 8

Trong đó, số 5 và số 3 là hai số hạng và tổng của chúng là 8.

Tương tự như khái niệm của số hạng, số hạng chưa biết là một thành phần trong một tổng hoặc một phép tính cộng nhưng giá trị của nó chưa được xác định. Thay vì biết trước giá trị cụ thể, chúng ta sử dụng một biến hoặc ký hiệu để đại diện cho số hạng đó.

Ví dụ: x + 7 =13

Trong đó: x là số hạng mà ta chưa biết, 7 là số hạng và 13 là tổng của x và 7.

Tính chất của một số hạng

• Tính chất giao hoán: Thứ tự các số hạng không ảnh hưởng đến kết quả của phép cộng. Ví dụ: 3 + 5 = 5 + 3.
• Tính chất kết hợp: Khi cộng các số hạng theo một thứ tự nhất định, kết quả không thay đổi. Ví dụ: (2 + 4) + 6 = 2 + (4 + 6). Kết quả của phép cộng không thay đổi dù ta nhóm các số hạng theo cách khác nhau.
• Tính chất phần tử đơn vị: Tồn tại một số hạng đặc biệt gọi là số 0, khi cộng với mọi số hạng khác, không làm thay đổi giá trị của số hạng đó. Ví dụ: 7 + 0 = 7.
• Tính chất số nghịch đảo: Đối với mỗi số hạng a, tồn tại một số hạng đối của nó (-a) sao cho a + (-a) = 0. Ví dụ (-8) + 8 = 0.

Phương pháp tìm một số hạng chưa biết

Để có thể tìm số hạng chưa biết trong một tổng, ta sẽ lấy tổng số của phép tính trừ đi số hạng đã biết. Từ đó, kết quả của phép trừ chính là số hạng chưa biết ta cần tìm.

Ví dụ: Tìm x trong phép tính sau:

x + 4 = 6

Áp dụng phương pháp đã nêu ở trên, ta có:

⇔ x = 6 - 4 = 2. Vậy x = 2 là số hạng chưa biết mà ta cần tìm.

Bài tập

Bài 1: Tìm x trong các phép tính dưới đây:

x + 3 = 12

6 + x = 7

9 + x = 13

x + 5 = 10

x + 2 = 11

Gợi ý lời giải:

x + 3 = 12

x = 12 - 3

x = 9

6 + x = 7

x = 7 - 6

x = 1

9 + x = 13

x = 13 - 9

x = 4

x + 5 = 10

x = 10 - 5

x = 5

x + 2 = 11

x = 11 - 2

x = 9

Bài 2: Lớp 2C có 29 bạn học sinh, trong lớp đó có 14 học sinh nữ. Hỏi lớp 2C có bao nhiêu bạn học sinh nam?

Gợi ý lời giải:

Số bạn học sinh nam ở lớp 2C là:

29 - 14 = 15 (bạn)

Đáp số: 15 bạn học sinh.

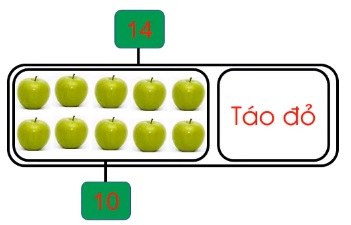
Bài 3: Một túi có 14 quả táo gồm táo xanh và táo đỏ, trong đó có 10 quả táo xanh. Hỏi có bao nhiêu quả táo đỏ?

Gợi ý lời giải:

Số táo đỏ bằng tổng số táo trừ đi số táo xanh.

Số táo đỏ có trong túi là:

14 - 10 = 4 (quả)

Đáp số: 4 quả táo đỏ.

Bài 4: Hai bến đò có tất cả 25 thuyền để chở khách đi tham quan, trong đó bến thứ nhất có 13 thuyền. Hỏi bến thứ hai có bao nhiêu thuyền?

Gợi ý lời giải:

Bến thứ hai có số thuyền là:

25 - 13 = 12 (thuyền)

Đáp số: 25 thuyền.

Bài 5: Trong sân trường, có tất cả 15 cây xanh được trồng trong sân, bác bảo vệ nói rằng có 6 cây bàng, những cây còn lại là cây phượng. Hỏi trên sân trường có bao nhiêu cây phượng?

Gợi ý lời giải:

Số cây phượng được trồng trong sân trường là:

15 - 6 = 9 (cây)

Đáp số: 9 cây phượng.

Như vậy, số hạng chưa biết là một khái niệm toán học quan trọng, đặc biệt là trong chương trình toán lớp 2. Nó mang nhiều tính chất linh hoạt giúp chúng ta dễ dàng áp dụng để giải nhiều dạng toán khác nhau. Các bạn học sinh cần hiểu và biết cách vận dụng thật tốt các tính chất và ứng dụng của số hạng chưa biết, bởi ngoài giúp chúng ta giải các bài toán ra, nó cũng giúp ta phát triển tư duy logic.

Hãy ôn tập thật tốt để nắm rõ các tính chất và phương pháp để giải toán, đồng thời luyện tập trí não có tư duy thật tốt các bạn nhé.