Dùng công thức Hê-rông tính diện tích tam giác bằng máy tính cầm tay

Trong các công thức tính diện tích tam giác có công thức Hê-rông sau:

Diện tích tam giác có độ dài 3 cạnh $a, b, c$ là $S=\sqrt{p(p-a)(p-b)(p-c)}$ trong đó $p=\dfrac{a+b+c}{2}$ là nửa chu vi của tam giác.

Ví dụ. Tính diện tích tam giác $ABC$ biết 3 cạnh của nó là $AB=a,$ $AC=\dfrac{a}{2},$ $BC=\dfrac{a\sqrt{7}}{2}.$

Giải. Nửa chu vi tam giác là $p=\dfrac{1}{2}a\left(1+\dfrac{1}{2}+\dfrac{\sqrt{7}}{2}\right)$

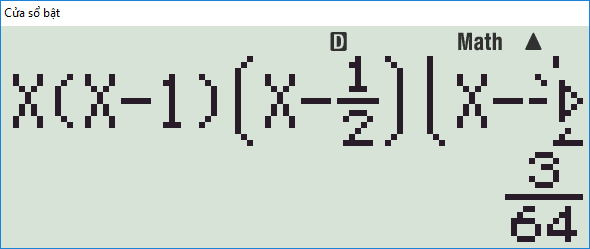
Diện tích tam giác $ABC$ là $S=\sqrt{p(p-a)\left(p-\frac{a}{2}\right)\left(p-\dfrac{a\sqrt{7}}{2}\right)}=\sqrt{\dfrac{3}{64}a^4}=\dfrac{a^2\sqrt{3}}{8}$

Các em chỉ cần trình bày lời giải vào giấy thi như trên thôi, không cần viết số cụ thể vào giấy đâu mà vẫn được điểm tối đa.

Bấm máy. Ta chỉ bấm phần số, sau khi được kết qua ta viết thêm $a$ vào, nếu độ dài thì viết thêm $a$, diện tích thì $a^2$, thể tích thì $a^3.$

• Nhập vào $\dfrac{1}{2}\left(1+\dfrac{1}{2}+\dfrac{\sqrt{7}}{2}\right)$ rồi nhấn SHIF RCL X để lưu kết quả vào biến nhớ X.

• Nhập vào $X(X-1)\left(X-\dfrac{1}{2}\right)\left(X-\dfrac{\sqrt{7}}{2}\right)$ rồi bấm bằng và đọc kết quả.

• Viết thêm $a^4$ vào kết quả và cho vào trong căn, lấy căn ta được diện tích tam giác.

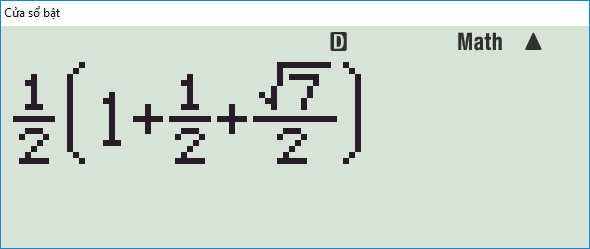
Cách bấm khác. Nếu độ dài các cạnh là kết quả khá phức tạp thì ta có thể lưu độ dài các cạnh vào các biến nhớ A, B, C của máy tính rồi nhập vào biểu thức X(X-A)(X-B)(X-C).

Bài tập thực thành. Tính diện tích tam giác $ABC$ biết:

1. $AB=4a\sqrt{2},$ $AC=a\sqrt{26},$ $BC=a\sqrt{10}.$
2. $AB=\dfrac{a}{2},$ $AC=\dfrac{a\sqrt{3}}{2},$ $BC=\dfrac{a}{2}.$
3. $AB=a\sqrt{2},$ $AC=4a,$ $BC=a\sqrt{10}.$
4. $AB=2a,$ $AC=3a,$ $BC=a\sqrt{13-6\sqrt{3}}.$

Đáp số:

1. $S=8a^2$
2. $S=\dfrac{a^2\sqrt{3}}{4}$
3. $S=2a^2$
4. $S=\dfrac{3}{2}a^2$

Công thức Hê-rông rất hiệu quả trong việc tính khoảng cách từ một điểm đến mặt phẳng mà ta không cần phải dựng đoạn vuông góc từ điểm đến mặt phẳng đó.

XEM TIẾP: Tính khoảng cách từ điểm đến mặt phẳng bằng thể tích tứ diện.